Great Stellated Dodecahedron Calculation
Online calculator and formulas for calculating a great stellated dodecahedron
This function calculates the height or volume of a great stellated dodecahedron.
To perform the calculation select the property you know and enter its value. Then click on 'Calculate'.
|
Great Stellated Dodecahedron Formulas
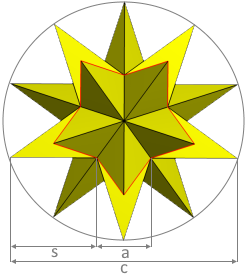
Edge length (\(\small{s}\))
\(\displaystyle s = \frac{a}{2} \cdot (1 + \sqrt{5})\) \(\displaystyle \;\;\; ≈ a \cdot 1.618\)
Chord length (\(\small{c}\))
\(\displaystyle c = a \cdot (2 + \sqrt{5})\) \(\displaystyle \;\;\; ≈ a \cdot 4.236\)
Volume (\(\small{V}\))
\(\displaystyle V=\frac{5}{4} \cdot a^3 \cdot (3 + \sqrt{5})\) \(\displaystyle \;\;\; ≈ a^3 \cdot 6.545\)
Surface area (\(\small{S}\))
\(\displaystyle S= 15\cdot a^2 \cdot \sqrt{5 + 2 \cdot \sqrt{5}}\) \(\displaystyle \;\;\; ≈ a^2 \cdot 46.165\)
Circumference Radius (\(\small{r}\))
\(\displaystyle r=\frac{a}{4} \cdot \sqrt{3} \cdot (3 + \sqrt{5})\) \(\displaystyle \;\;\; ≈ a \cdot 2.267\)
Height (\(\small{h}\))
\(\displaystyle h = \frac{a}{6} \cdot \sqrt{3} \cdot (3 + \sqrt{5})\) \(\displaystyle \;\;\; ≈ a \cdot 1.512 \)
Cuboid
•
Square Pillar
•
Antiprism
•
Hexagonal prism
•
Triangular prism
•
Regular prism
•
Oblique prism
•
Ramp
•
Anticube
•
Wedge
•
Right Wedge
•
Rhombohedron
•
Parallelepiped
•
Tetrahedron, irregular
•
Tetragonal Trapezohedron
•
Pentagonal Trapezohedron
•
Prismatoid
•
Stellated Octahedron
•
Stellated Dodecahedron
•
Great Stellated Dodecahedron
•
Great Dodecahedron
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron
|
|