Stellated Octahedron Calculator
Online calculator and formulas for calculating a Stellated Octahedron
Stellated Octahedron Calculator
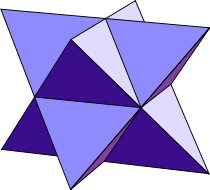
The Stellated Octahedron
A Stellated Octahedron is a star polyhedron formed by extending the faces of a regular octahedron.
Stellated Octahedron Properties
The 3D Star: Eight triangular pyramids on octahedron faces
|
|
What is a Stellated Octahedron?
A Stellated Octahedron is a fascinating star polyhedron:
- Definition: Compound of two intersecting tetrahedra
- Formation: Extension of octahedron faces to pyramids
- Star Shape: Eight-pointed three-dimensional star
- Vertices: 6 star points
- Faces: 8 triangular faces
- Symbol: Also called Stella Octangula
Geometric Properties of the Stellated Octahedron
The Stellated Octahedron exhibits remarkable geometric properties:
Star Properties
- Compound: Two interpenetrating tetrahedra
- Faces: 8 equilateral triangles
- Euler Formula: V - E + F = 6 - 12 + 8 = 2
- Symmetry: Same as regular octahedron
Special Properties
- Kepler's Star: First stellation discovered
- Self-intersecting: Faces pass through interior
- Dual Relation: Related to cube stellation
- Uniform Edges: All edges equal length
Mathematical Relationships
The Stellated Octahedron follows elegant mathematical laws:
Volume Formula
Based on edge length and square root of 2. Elegant and precise.
Surface Formula
Area of eight equilateral triangles. Perfect triangular symmetry.
Applications of the Stellated Octahedron
Stellated Octahedra find applications in various fields:
Architecture & Design
- Star-shaped architectural elements
- Decorative building features
- Modern geometric facades
- Sculptural installations
Science & Technology
- Crystal structure studies
- Molecular geometry models
- Antenna design patterns
- Optical component shapes
Education & Research
- Geometry education tools
- 3D visualization studies
- Mathematical demonstrations
- Polyhedron theory research
Art & Crafts
- Star-shaped sculptures
- Origami models
- Jewelry design elements
- Decorative objects
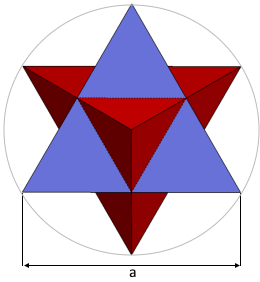
Stellated Octahedron Formulas
Edge Length (b)
Where a is the outer edge length
Volume (V)
Volume with square root of 2
Surface Area (S)
Eight equilateral triangular faces
Circumference Radius (ru)
Radius of circumscribing sphere
Edge Circle Radius (rk)
Radius of edge-touching sphere
Inner Circle Radius (ri)
Radius of inscribed sphere
Calculation Example for Stellated Octahedron
Given
Find: All properties of the stellated octahedron
1. Volume Calculation
For a = 10:
\[V = \frac{10^3 \cdot \sqrt{2}}{8}\] \[V = \frac{1000 \cdot 1.414}{8}\] \[V ≈ 177\]The volume is approximately 177 cubic units
2. Surface Area Calculation
For a = 10:
\[S = \frac{3}{2} \cdot 100 \cdot \sqrt{3}\] \[S = 150 \cdot 1.732\] \[S ≈ 260\]The surface area is approximately 260 square units
3. Circumference Radius
For a = 10:
\[r_u = \frac{10 \cdot \sqrt{6}}{4}\] \[r_u = \frac{10 \cdot 2.449}{4}\] \[r_u ≈ 6.12\]The circumference radius is approximately 6.12 units
4. Inner Circle Radius
For a = 10:
\[r_i = \frac{10}{2 \cdot \sqrt{6}}\] \[r_i = \frac{10}{2 \cdot 2.449}\] \[r_i ≈ 2.04\]The inner circle radius is approximately 2.04 units
5. Complete Stellated Octahedron
The stellated octahedron with perfect eight-pointed star symmetry
The Stellated Octahedron: Kepler's Star Discovery
The Stellated Octahedron is one of the most beautiful and historically significant star polyhedra. Discovered by Johannes Kepler in 1619, it represents the first systematic exploration of stellar polyhedra. Also known as the "Stella Octangula" (eight-pointed star), this remarkable shape is formed by the compound of two tetrahedra, creating a three-dimensional Star of David that captivates mathematicians and artists alike.
The Geometry of Stellar Beauty
The Stellated Octahedron demonstrates the elegance of geometric stellation:
- Historical Significance: First star polyhedron discovered by Kepler
- Compound Structure: Two interpenetrating regular tetrahedra
- Perfect Symmetry: Maintains octahedral symmetry group
- Self-Intersection: Faces pass through the interior volume
- Dual Relationship: Related to cube compound structures
- Mathematical Elegance: Simple formulas with √2 and √3
- Visual Impact: Striking eight-pointed star appearance
Mathematical Elegance
Geometric Perfection
The formulas reveal the inherent mathematical beauty: volume proportional to √2, surface area to √3, creating perfect harmony between edge length and spatial properties.
Stellar Composition
As a compound of two tetrahedra, it demonstrates how simple regular solids can combine to create complex, beautiful forms with enhanced symmetry properties.
Historical Impact
Kepler's discovery opened the door to an entire family of star polyhedra, revolutionizing our understanding of three-dimensional geometry and inspiring centuries of mathematical research.
Artistic Inspiration
The stellated octahedron's striking appearance has influenced art, architecture, and design, serving as a symbol of geometric harmony and mathematical beauty.
Summary
The Stellated Octahedron stands as a testament to the beauty of mathematical discovery. From Kepler's initial fascination to modern applications in crystal structure and design, this remarkable star polyhedron continues to inspire wonder and study. Its elegant formulas, perfect symmetry, and striking visual impact make it one of the most beloved shapes in all of geometry. As both a historical milestone and a continuing source of mathematical insight, the stellated octahedron bridges the gap between pure mathematical theory and aesthetic appreciation, proving that in mathematics, beauty and truth are often one and the same.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron