Regular Tetrahedron Calculator

Online calculator and formula for calculating the properties of a tetrahedron

The Simplest Platonic Solid - Perfect Triangular Symmetry!

Tetrahedron Calculator

The Regular Tetrahedron

The regular tetrahedron is the simplest Platonic solid with 4 equilateral triangular faces.

Enter Known Parameters
Which parameter is known?
Value of the selected parameter
Tetrahedron Calculation Results
Side length a:
Volume V:
Surface S:
Height h:
Platonic Solid Properties

The simplest Platonic solid: Four equilateral triangular faces

4 triangular faces 4 vertices 6 edges Perfect symmetry

Tetrahedron Structure

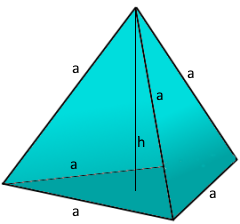
Regular Tetrahedron

The simplest 3D geometric form.
Platonic solid with perfect symmetry.

What is a Regular Tetrahedron?

The regular tetrahedron is the fundamental Platonic solid:

  • Definition: Simplest Platonic solid
  • Faces: 4 equilateral triangles
  • Vertices: 4 vertices
  • Edges: 6 edges (all equal)
  • Symmetry: Tetrahedral symmetry
  • Dual: Self-dual polyhedron

Geometric Properties of the Tetrahedron

The regular tetrahedron shows fundamental geometric properties:

Basic Parameters
  • Faces: 4 equilateral triangles
  • Vertices: 4 vertices
  • Edges: 6 edges (all equal length)
  • Euler characteristic: V - E + F = 4 - 6 + 4 = 2
Special Properties
  • Platonic solid: One of the 5 Platonic solids
  • Self-dual: Dual to itself
  • Simplest 3D form: Minimum vertices and faces
  • Tetrahedral symmetry: Td symmetry group

Mathematical Relationships

The regular tetrahedron follows elegant mathematical laws:

Volume Formula
With √2 factor

Contains the square root of 2. Simple and elegant.

Surface Formula
With √3 factor

4 equilateral triangles. Classic √3 relationship.

Applications of the Tetrahedron

Regular tetrahedra find applications in various fields:

Architecture & Engineering
  • Triangular truss structures
  • Space frame construction
  • Structural supports
  • Geodesic dome elements
Science & Technology
  • Molecular geometry (CH₄)
  • Crystal structures
  • Optical prisms
  • Chemical bonding models
Education & Teaching
  • Basic 3D geometry
  • Platonic solids introduction
  • Symmetry studies
  • Mathematical demonstrations
Art & Design
  • Minimalist sculptures
  • Modern art installations
  • Geometric patterns
  • 3D printed objects

Regular Tetrahedron Formulas

Volume (V)
\[V = \frac{a^3}{12} \cdot \sqrt{2} \approx 0.1179 \cdot a^3\]

Volume with √2 factor for tetrahedral geometry

Surface (S)
\[S = a^2 \cdot \sqrt{3} \approx 1.732 \cdot a^2\]

4 equilateral triangles with √3 relationship

Height (h)
\[h = \frac{a}{3} \cdot \sqrt{6} \approx 0.8165 \cdot a\]

Height with √6 for optimal proportions

Platonic Solid
Tetrahedron - Fire Element

Associated with fire in classical elements

Tetrahedron Parameters
Faces
4 equilateral △
Vertices
4 vertices
Edges
6 edges
Symmetry
Td

All properties follow from the perfect triangular symmetry

Calculation Example for a Regular Tetrahedron

Given
Side length a = 10 Platonic solid

Find: All properties of the regular tetrahedron

1. Volume Calculation

For a = 10:

\[V = \frac{10^3}{12} \cdot \sqrt{2}\] \[V ≈ \frac{1000}{12} \cdot 1.414\] \[V ≈ 117.9\]

The volume is approximately 117.9 cubic units

2. Surface Calculation

For a = 10:

\[S = 10^2 \cdot \sqrt{3}\] \[S ≈ 100 \cdot 1.732\] \[S ≈ 173.2\]

The surface area is approximately 173.2 square units

3. Height Calculation

For a = 10:

\[h = \frac{10}{3} \cdot \sqrt{6}\] \[h ≈ 3.33 \cdot 2.449\] \[h ≈ 8.165\]

The height is approximately 8.165 units

4. The Perfect Tetrahedron
Side length a = 10.0 Volume V ≈ 117.9 Surface S ≈ 173.2
Height h ≈ 8.17 4 Triangles △ 🔥 Fire Element

The regular tetrahedron with perfect tetrahedral symmetry

The Regular Tetrahedron: Foundation of 3D Geometry

The regular tetrahedron stands as the most fundamental three-dimensional form, representing the simplest possible polyhedron with triangular faces. As the first of the five Platonic solids, it embodies the perfect balance between mathematical elegance and geometric simplicity. Its four equilateral triangular faces, six equal edges, and four vertices create a structure of such symmetry and beauty that it has fascinated mathematicians, philosophers, and scientists for millennia, from ancient Greece to modern molecular chemistry.

The Geometry of Fundamental Simplicity

The regular tetrahedron showcases fundamental geometric principles:

  • Minimal complexity: Fewest faces, edges, and vertices for a 3D solid
  • Self-dual property: Its dual polyhedron is another tetrahedron
  • Tetrahedral symmetry: Td symmetry group with 24 operations
  • Equilateral faces: All four faces are congruent equilateral triangles
  • Platonic heritage: Associated with fire in classical elements
  • Mathematical beauty: Simple √2, √3, and √6 relationships
  • Universal presence: From molecules to architectural structures

Mathematical and Scientific Significance

Chemical Perfection

The tetrahedral geometry is fundamental in chemistry, particularly in carbon compounds like methane (CH₄), where the carbon atom sits at the center with four hydrogen atoms at the vertices.

Structural Foundation

The triangular faces provide maximum stability with minimum material, making the tetrahedron essential in structural engineering and space frame construction.

Mathematical Elegance

The tetrahedron's formulas demonstrate the beauty of mathematical relationships, with each property connected through elegant square root expressions.

Educational Foundation

As the simplest 3D form, it serves as the perfect introduction to three-dimensional geometry, symmetry, and the concept of Platonic solids.

Summary

The regular tetrahedron represents the perfect synthesis of mathematical simplicity and geometric beauty. As the foundation of three-dimensional geometry and the first Platonic solid, it demonstrates how minimal complexity can achieve maximum elegance. From its role in molecular chemistry to its applications in architecture and engineering, the tetrahedron continues to serve as both a fundamental building block and a source of inspiration. Its elegant √2, √3, and √6-based formulas reveal the deep mathematical relationships that govern three-dimensional space, while its tetrahedral symmetry provides a perfect example of how nature and mathematics converge in forms of extraordinary beauty and functionality. Whether studied as an abstract mathematical object or appreciated for its practical applications, the regular tetrahedron remains the essential starting point for understanding the geometry of three-dimensional space.