Dodecahedron Calculator

Online calculator and formulas for calculating the properties of a dodecahedron

The Golden Pentagon - Platonic Perfection with φ!

Dodecahedron Calculator

The Regular Dodecahedron

A dodecahedron is a platonic solid with 12 pentagonal faces, 20 vertices, and 30 edges.

Enter Known Parameters
Which parameter is known?
Value of the selected parameter
Dodecahedron Calculation Results
Side length a:
Volume V:
Surface S:
Diagonal d:
Height h:
Circumradius Rc:
Midradius Rm:
Inradius Ri:
Platonic Solid Properties

The Golden Pentagon Polyhedron: Most complex of the five platonic solids

12 pentagonal faces 20 vertices 30 edges Golden ratio φ

Dodecahedron Structure

Dodecahedron

The most complex platonic solid with 12 pentagonal faces.
Embodies the golden ratio φ in its geometry.

What is a Dodecahedron?

A dodecahedron is the most complex of the five platonic solids:

  • Definition: 12 congruent pentagonal faces
  • Platonic Solid: Perfect regular polyhedron
  • Faces: 12 regular pentagons
  • Vertices: 20 corners
  • Edges: 30 equal edges
  • Golden Ratio: φ = (1+√5)/2 ≈ 1.618

Geometric Properties of the Dodecahedron

The dodecahedron demonstrates the most sophisticated geometric relationships:

Basic Parameters
  • Faces: 12 regular pentagons
  • Vertices: 20 corners (3 faces meet)
  • Edges: 30 edges (all equal length)
  • Euler characteristic: V - E + F = 20 - 30 + 12 = 2
Special Properties
  • Golden ratio: All proportions involve φ
  • Pentagon angles: Each interior angle is 108°
  • Regular faces: All faces are regular pentagons
  • Dual polyhedron: Dual to the icosahedron

Mathematical Relationships

The dodecahedron embodies the golden ratio in all its mathematical relationships:

Volume Formula
With (15+7√5)/4

Complex formula involving √5. Golden ratio embedded.

Surface Formula
With √(25+10√5)

12 regular pentagons. Golden ratio relationships.

Applications of the Dodecahedron

Dodecahedrons appear in nature, science, and human design due to their golden ratio properties:

Nature & Biology
  • Virus capsid structures
  • Organic crystal formations
  • Plant growth patterns
  • Molecular geometry
Science & Technology
  • Crystal structures and mineralogy
  • Quantum fullerene research
  • 3D modeling and CAD
  • Optical and acoustic applications
Education & Mathematics
  • Golden ratio demonstrations
  • Advanced geometry studies
  • Platonic solids theory
  • Mathematical modeling
Games & Art
  • 12-sided gaming dice (d12)
  • Artistic sculptures and installations
  • Architectural design elements
  • Puzzle and brain teaser designs

Dodecahedron Formulas

Volume (V)
\[V=\frac{a^3}{4} \cdot (15+7\sqrt{5})\]

Complex formula with golden ratio embedded through √5

Surface Area (S)
\[S= 3a^2 \sqrt{25+10\sqrt{5}}\]

12 regular pentagons with golden ratio relationships

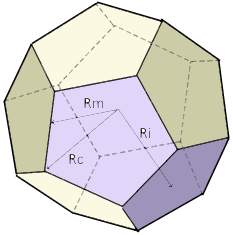
Circumradius (Rc)
\[R_c=\frac{a}{4} \sqrt{3}(1+\sqrt{5})\]

Radius to vertices, involving golden ratio φ

Midradius (Rm)
\[R_m=\frac{a}{4} (3 +\sqrt{5})\]

Radius to edge midpoints

Inradius (Ri)
\[R_i=\frac{a}{2} \sqrt{\frac{25+11\sqrt{5}}{10}}\]

Radius to face centers

Diagonal & Height
\[d = 2R_c\]
\[h = 2R_i\]

Simple relationships to radii

Golden Ratio Connection
Golden Ratio:
\(\phi = \frac{1+\sqrt{5}}{2} \approx 1.618\)
Pentagon Angle:
108° = 3π/5
Face Diagonal:
\(a \cdot \phi\)

All dodecahedron properties are intimately connected to the golden ratio φ

Calculation Example for a Dodecahedron

Given
Side length a = 10 Golden Ratio φ ≈ 1.618

Find: All properties of the dodecahedron

1. Volume Calculation

For a = 10:

\[V = \frac{10^3}{4} \cdot (15+7\sqrt{5})\] \[V = 250 \cdot (15+7 \times 2.236)\] \[V ≈ 250 \times 30.652 ≈ 7663\]

The volume is approximately 7663 cubic units

2. Surface Area Calculation

For a = 10:

\[S = 3 \times 10^2 \sqrt{25+10\sqrt{5}}\] \[S = 300 \sqrt{25+22.36}\] \[S ≈ 300 \times 6.881 ≈ 2064\]

The surface area is approximately 2064 square units

3. Circumradius Calculation

For a = 10:

\[R_c = \frac{10}{4} \sqrt{3}(1+\sqrt{5})\] \[R_c = 2.5 \times 1.732 \times 3.236\] \[R_c ≈ 14.01\]

The circumradius is approximately 14.01 units

4. Inradius Calculation

For a = 10:

\[R_i = \frac{10}{2} \sqrt{\frac{25+11\sqrt{5}}{10}}\] \[R_i = 5 \sqrt{\frac{49.57}{10}}\] \[R_i ≈ 5 \times 2.226 ≈ 11.13\]

The inradius is approximately 11.13 units

5. Complete Dodecahedron Properties
Side a = 10.0 Volume V ≈ 7663 Surface S ≈ 2064
Circumradius Rc ≈ 14.01 Inradius Ri ≈ 11.13 🌟 φ-Perfect

The dodecahedron with perfect golden ratio relationships

The Dodecahedron: Sacred Geometry of the Golden Ratio

The dodecahedron stands as the most sophisticated and mystical of the five Platonic solids, embodying the golden ratio φ in every aspect of its geometry. With its 12 pentagonal faces, 20 vertices, and 30 edges, it represents the pinnacle of geometric complexity and mathematical beauty. Ancient Greek philosophers, particularly Plato, associated the dodecahedron with the universe itself, believing its divine proportions reflected the cosmic order. The mathematical elegance lies in how every measurement, angle, and relationship involves the golden ratio, making it a perfect study of how nature's most fundamental constant manifests in three-dimensional space.

The Geometry of Divine Proportion

The dodecahedron exemplifies the golden ratio in geometric form:

  • Platonic Solid: The most complex of the five regular polyhedra
  • Icosahedral Symmetry: Perfect Ih symmetry group
  • Golden Pentagon: All faces are regular pentagons with φ relationships
  • φ-Proportions: Every measurement involves the golden ratio
  • Dual Polyhedron: Dual to the icosahedron (20 faces ↔ 20 vertices)
  • Sacred Geometry: Associated with the cosmos in ancient philosophy
  • Natural Occurrence: Found in virus structures and crystal forms

Mathematical Mystique

Golden Ratio Omnipresence

Every formula contains √5, connecting directly to φ = (1+√5)/2. The dodecahedron is essentially a 3D manifestation of the golden ratio's geometric power.

Pentagon Perfection

Its 12 pentagonal faces each contain the golden ratio in their proportions, with diagonals to sides in φ:1 ratio, creating infinite recursive beauty.

Cosmic Symbolism

Ancient Greeks believed the dodecahedron represented the universe, with its 12 faces possibly corresponding to the zodiac or cosmic cycles.

Modern Applications

From virus capsids to fullerene chemistry, from gaming dice to architectural design, the dodecahedron bridges ancient wisdom with modern science.

Summary

The dodecahedron represents the culmination of Platonic perfection, where mathematical complexity meets aesthetic beauty through the golden ratio. Its intricate formulas, all involving √5 and thus φ, demonstrate how a single constant can generate infinite geometric relationships. From its ancient association with cosmic order to its modern applications in chemistry and design, the dodecahedron continues to fascinate mathematicians, scientists, and artists alike. As the most complex regular polyhedron, it serves as a bridge between the earthly simplicity of the cube and the cosmic complexity of natural forms. Its 12 pentagonal faces remind us that perfection often emerges from complexity, and that the most profound mathematical truths are often the most beautiful.