Tetragonal Trapezohedron Calculator
Calculator and formulas for a tetragonal trapezohedron
Tetragonal Trapezohedron Calculator
The Tetragonal Trapezohedron
A Trapezohedron is a twisted double pyramid rotated by 180°/n (deltohedron).
Tetragonal Trapezohedron Properties
The Twisted Double Pyramid: Eight kite-shaped faces, twisted by 45°
Tetragonal Trapezohedron Structure
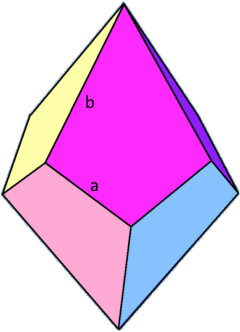
The twisted double pyramid with kite-shaped faces.
Also known as deltohedron.
|
|
What is a Tetragonal Trapezohedron?
A Tetragonal Trapezohedron is a fascinating twisted polyhedron:
- Definition: Twisted double pyramid (deltohedron)
- Formation: Two square pyramids twisted by 45°
- Faces: Eight congruent kite-shaped faces
- Vertices: 10 vertices total
- Edges: 16 edges (8+8)
- Twist: 180°/4 = 45° rotation
Geometric Properties of the Tetragonal Trapezohedron
The Tetragonal Trapezohedron shows remarkable geometric features:
Basic Properties
- Faces: 8 congruent kite shapes
- Base: Two square faces (top and bottom)
- Twist Angle: 45° rotation between bases
- Symmetry: 4-fold rotational axis
Special Properties
- Deltohedron: All faces are kites (deltas)
- Chiral: Exists in left and right forms
- Crystal Form: Common in mineral crystals
- Dual: Self-dual polyhedron family
Mathematical Relationships
The Tetragonal Trapezohedron follows complex mathematical laws:
Volume Formula
Based on antiprism length z with nested square roots. Elegant but complex.
Surface Formula
Sum of eight congruent kite areas. Perfect deltoidal symmetry.
Applications of the Tetragonal Trapezohedron
Tetragonal Trapezohedra find applications in various fields:
Mineralogy & Crystals
- Natural crystal formations
- Garnet crystal structures
- Diamond crystal habits
- Crystallographic studies
Gaming & Recreation
- Ten-sided dice (d10)
- Gaming accessories
- Probability games
- Educational tools
Architecture & Design
- Twisted building elements
- Decorative architectural features
- Modern sculptural designs
- Geometric art installations
Science & Research
- Molecular geometry models
- Crystal structure analysis
- Materials science research
- Optical component design
Tetragonal Trapezohedron Formulas
Reference Parameter
Length of the antiprism = z (fundamental parameter)
Side Length (a)
Short edge of kite faces
Side Length (b)
Long edge of kite faces
Height (h)
Distance between parallel faces
Surface Area (S)
Total area of eight kite faces
Volume (V)
Volume of the twisted double pyramid
Calculation Example for Tetragonal Trapezohedron
Given
Find: All properties of the tetragonal trapezohedron
1. Side Length Calculations
For z = 10:
\[a = \sqrt{\sqrt{2} - 1} \cdot 10 ≈ 6.44\] \[b = 1.0987 \cdot 10 ≈ 10.99\]Short edge a ≈ 6.44, Long edge b ≈ 10.99
2. Height Calculation
For z = 10:
\[h = \sqrt{\frac{1}{2} \cdot (4 + 3\sqrt{2})} \cdot 10\] \[h ≈ 2.03 \cdot 10 ≈ 20.3\]The height is approximately 20.3 units
3. Surface Area Calculation
For z = 10:
\[S = 2\sqrt{2 + 4\sqrt{2}} \cdot 100\] \[S ≈ 5.5342 \cdot 100 ≈ 553\]The surface area is approximately 553 square units
4. Volume Calculation
For z = 10:
\[V = \frac{1}{3}\sqrt{4 + 3\sqrt{2}} \cdot 1000\] \[V ≈ 0.957 \cdot 1000 ≈ 957\]The volume is approximately 957 cubic units
5. Complete Tetragonal Trapezohedron
The tetragonal trapezohedron with perfect twisted symmetry
The Tetragonal Trapezohedron: Nature's Twisted Gem
The Tetragonal Trapezohedron represents one of nature's most elegant geometric forms, combining the stability of pyramidal structures with the dynamic beauty of twisted symmetry. Also known as a deltohedron due to its kite-shaped faces, this remarkable polyhedron appears frequently in crystalline structures and serves as the foundation for the familiar ten-sided dice used in gaming and probability studies.
The Geometry of Twisted Perfection
The Tetragonal Trapezohedron demonstrates the beauty of controlled geometric twist:
- Twisted Structure: Two square pyramids rotated 45° relative to each other
- Kite Faces: Eight congruent kite-shaped faces with perfect symmetry
- Natural Occurrence: Common in garnet, diamond, and other crystal systems
- Gaming Applications: The standard ten-sided die (d10) shape
- Mathematical Beauty: Complex formulas involving nested square roots
- Chiral Properties: Exists in left-handed and right-handed forms
- Deltoidal Symmetry: Perfect balance of acute and obtuse angles
Mathematical Elegance
Complex Square Root Relationships
The formulas reveal intricate mathematical relationships involving nested square roots of 2, creating a beautiful hierarchy of geometric proportions that govern all dimensions.
Crystallographic Significance
As a common crystal habit, the tetragonal trapezohedron bridges pure mathematics and natural science, appearing in numerous mineral formations with perfect geometric precision.
Gaming Heritage
The ten-sided die based on this shape has been used for centuries in games and divination, making it one of the most practically important polyhedra in human culture.
Architectural Inspiration
Modern architects draw inspiration from its twisted form, creating buildings and structures that capture the dynamic tension between stability and movement.
Summary
The Tetragonal Trapezohedron stands as a testament to the profound connection between mathematical theory and natural beauty. From its origins in crystal formations to its modern applications in gaming and architecture, this twisted polyhedron continues to fascinate scholars and practitioners alike. Its complex formulas, involving elegant square root relationships, describe not just geometric properties but reveal the underlying mathematical harmonies that govern natural crystal growth. As both a theoretical mathematical object and a practical tool for probability and design, the tetragonal trapezohedron exemplifies how geometric perfection emerges from the interplay of symmetry, proportion, and the fundamental constants of mathematics.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron