Antiprism Calculator
Calculator and formulas for calculating an antiprism
Antiprism Calculator
The Antiprism
An Antiprism is a prismatic body with twisted base faces (by 180°/n).
Antiprism Properties
The Twisted Prism: Base faces rotated by 180°/n
Antiprism Structure
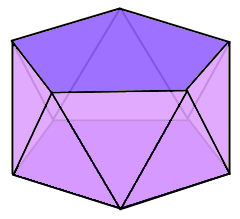
The twisted prism with rotated base faces.
Rotation by 180°/n.
|
|
What is an Antiprism?
An Antiprism is a fascinating prismatic body:
- Definition: Prism with twisted base faces
- Rotation: Top base rotated by 180°/n
- Side faces: 2n congruent triangles
- Vertices: 2n vertices total
- Edges: 4n edges (n+n+2n)
- Regular: All edges equal length
Geometric Properties of the Antiprism
The Antiprism exhibits remarkable geometric properties:
Basic Parameters
- Base faces: 2 regular n-gons
- Side faces: 2n congruent triangles
- Euler Characteristic: V - E + F = 2n - 4n + (2n+2) = 2
- Rotation angle: 180°/n
Special Properties
- Chiral object: Exists in left and right forms
- Uniform edges: All edges equal length
- Rotational symmetry: n-fold rotation axis
- Semiregular: Two types of faces
Mathematical Relationships
The Antiprism follows complex trigonometric laws:
Volume Formula
Depends on cos, sin and n. Complex but elegant.
Surface Formula
Sum of base faces and triangles. Elegant trigonometric form.
Applications of the Antiprism
Antiprisms find applications in various fields:
Architecture & Construction
- Twisted tower structures
- Modern building designs
- Structural bracing systems
- Architectural elements
Science & Technology
- Crystallographic structures
- Molecular geometry
- Optical components
- Mechanical constructions
Education & Teaching
- Geometry instruction
- Trigonometry applications
- 3D geometry studies
- Mathematical demonstrations
Art & Design
- Sculptural works
- Art installations
- Decorative objects
- Geometric patterns
Formulas for the Antiprism
Surface Area (S)
Surface area with cotangent and √3
Volume (V)
Complex trigonometric volume formula
Height (h)
Height dependent on vertex count n
Important Note
Angle functions require radian mode
Antiprism Parameters
2 regular n-gons
2n triangles
180°/n
All equal length
All properties depend on the vertex count n of the base
Calculation Example for an Antiprism
Given
Find: All properties of the pentagonal antiprism
1. Surface Area Calculation
For n=5:
\[S = \frac{5}{2} \cdot (\cot(36°) + \sqrt{3}) \cdot 100\] \[S ≈ 2.5 \cdot (1.376 + 1.732) \cdot 100\] \[S ≈ 777\]The surface area is approximately 777 square units
2. Height Calculation
For n=5:
\[h = \sqrt{1 - \frac{1}{4 \cdot \cos^2(18°)}} \cdot 10\] \[h ≈ \sqrt{1 - 0.277} \cdot 10\] \[h ≈ 8.5\]The height is approximately 8.5 length units
3. The Pentagonal Antiprism
The pentagonal antiprism with perfect rotational symmetry
The Antiprism: The Twisted Prism
The Antiprism is a fascinating geometric body that embodies the elegance of rotation. Through the characteristic rotation of the upper base by 180°/n, it creates a unique structure with 2n triangular side faces, making the antiprism one of the most interesting semiregular polyhedra. The mathematical beauty lies in the complex trigonometric relationships that connect all geometric properties, creating a perfect harmony between symmetry, rotation, and mathematical elegance.
The Geometry of Rotation
The antiprism demonstrates the perfection of geometric rotation:
- Rotation angle: Precisely 180°/n for n-gonal base
- Chirality: Exists in left and right forms
- Uniformity: All edges have the same length
- Semiregularity: Two different face types
- Symmetry: n-fold rotation axis
- Trigonometry: Complex sine and cosine relationships
- Versatility: Works for any vertex count n ≥ 3
Mathematical Elegance
Trigonometric Perfection
The antiprism formulas are masterpieces of trigonometry, showing how sine, cosine, and cotangent work together to describe the twisted geometry.
Parametric Diversity
By varying the vertex count n, infinitely many different antiprisms arise, from triangular to highly polygonal forms with different aesthetic qualities.
Structural Innovation
The rotation creates optimal stress distribution, making antiprisms preferred structures in architecture and engineering.
Aesthetic Perfection
The harmonious combination of regular base faces and uniformly twisted triangles creates unique visual dynamics.
Summary
The Antiprism embodies the perfect balance between mathematical complexity and geometric beauty. Its twisted structure, described by elegant trigonometric formulas, makes it a fascinating study object for mathematicians, architects, and designers. From simple triangular forms to complex polygonal variants, the antiprism shows how rotation of basic forms can lead to entirely new geometric worlds. As a bridge between theoretical mathematics and practical application, the antiprism remains a fascinating example of the power of geometric transformation.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron