Great Dodecahedron Calculator
Calculator and formulas for calculating a great dodecahedron
Great Dodecahedron Calculator
The Great Dodecahedron
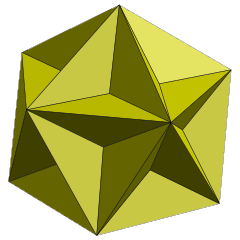
A great dodecahedron is a star polyhedron with twelve pentagonal star faces. It's one of the four Kepler-Poinsot polyhedra.
Great Dodecahedron Properties
The stellar polyhedron: Twelve pentagonal star faces intersecting through space
|
|
What is a Great Dodecahedron?
A great dodecahedron is one of the most fascinating star polyhedra:
- Definition: Star polyhedron with 12 pentagonal faces
- Classification: Kepler-Poinsot polyhedron
- Faces: Self-intersecting pentagonal stars
- Vertices: 20 vertices (shared with icosahedron)
- Nature: Non-convex and self-intersecting
- Dual: Small stellated dodecahedron
Geometric Properties of the Great Dodecahedron
The great dodecahedron displays remarkable stellar characteristics:
Stellar Parameters
- Faces: 12 pentagonal stars
- Edges: 30 edges
- Vertices: 20 vertices
- Genus: 4 (topological classification)
Special Properties
- Self-intersecting: Faces pass through interior
- Star density: Each face has density 3/2
- Kepler-Poinsot: One of four regular star polyhedra
- Golden ratio: All dimensions involve φ
Mathematical Relationships
The great dodecahedron follows complex mathematical laws involving the golden ratio:
Golden Ratio Formulas
All formulas involve the golden ratio. Complex but beautiful relationships.
Star Geometry
Each pentagonal face extends as a star. Creates beautiful intersection patterns.
Applications of the Great Dodecahedron
Great dodecahedra find applications in specialized fields:
Mathematics & Science
- Polyhedral research
- Crystallography studies
- Topology investigations
- Golden ratio studies
Art & Design
- Sculptural works
- 3D art installations
- Geometric patterns
- Artistic visualizations
Education & Research
- Advanced geometry courses
- Polyhedral studies
- Mathematical modeling
- Visual mathematics
Computer Graphics
- 3D rendering algorithms
- Game development
- Procedural generation
- Mathematical visualization
Great Dodecahedron Formulas
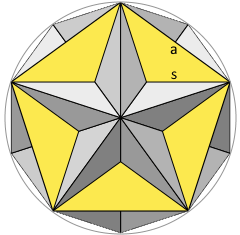
Side length (s)
Side length involves the golden ratio conjugate
Volume (V)
Volume formula with golden ratio factor
Surface area (S)
Complex surface area with nested radicals
Circumference Radius (r)
Radius of the circumscribed sphere
Pyramid height (h)
Height of pentagonal pyramid from center to face
Example calculation for a Great Dodecahedron
Given
Calculate: All properties of the great dodecahedron
1. Side length calculation
The side length is 6.18 units
2. Volume calculation
The volume is 1545 cubic units
3. Surface area calculation
The surface area is 1089 square units
4. Circumradius calculation
The circumradius is 9.51 units
Summary
A complete analysis of the great dodecahedron with edge length 10
The Great Dodecahedron: Master of Stellar Geometry
The great dodecahedron represents one of the most sophisticated achievements in polyhedral geometry. As one of the four Kepler-Poinsot polyhedra, it demonstrates the mathematical beauty that emerges when we extend beyond convex shapes into the realm of star polyhedra. Its twelve pentagonal star faces create a structure of extraordinary complexity and elegance, where self-intersection becomes a feature rather than a flaw.
The Poetry of Star Geometry
The great dodecahedron showcases the beauty of non-convex geometry:
- Star faces: Each pentagonal face extends as a five-pointed star
- Golden ratio: All proportions involve the divine ratio φ
- Self-intersection: Faces pass through the interior creating complex patterns
- Kepler-Poinsot: One of only four regular star polyhedra
- Dual relationship: Dual to the small stellated dodecahedron
- Icosahedral symmetry: Shares vertices with the icosahedron
- Mathematical elegance: Complex formulas with beautiful simplicity
Historical and Mathematical Significance
Kepler's Discovery
Johannes Kepler first described the great dodecahedron in 1619, extending the concept of regular polyhedra beyond the Platonic solids to include star forms.
Golden Ratio Mathematics
Every dimension and calculation involves the golden ratio, making it a perfect example of how φ appears throughout advanced geometry and nature.
Topological Wonder
With genus 4, the great dodecahedron demonstrates advanced topological properties, bridging elementary geometry and advanced mathematical concepts.
Artistic Inspiration
Its stellar beauty has inspired mathematicians, artists, and designers for centuries, representing the perfect marriage of mathematical rigor and aesthetic appeal.
Conclusion
The great dodecahedron stands as a testament to the infinite creativity possible within mathematical constraints. By extending the familiar dodecahedron into star form, we discover a universe of geometric possibilities that challenge our preconceptions about shape and space. Its self-intersecting faces create patterns of stunning complexity, while its golden ratio proportions connect it to the deepest harmonies of mathematics and nature. For students of advanced geometry, the great dodecahedron offers a gateway into the fascinating world of non-convex polyhedra, where mathematical beauty reaches new heights of sophistication and wonder. As both a mathematical object and an artistic inspiration, it continues to captivate those who encounter its stellar magnificence.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron