Antiwürfel Rechner
Rechner und Formeln zur Berechnung eines Antiwürfels
Antiwürfel Rechner
Der Antiwürfel
Ein Antiwürfel ist ein würfelartiger Körper mit um 45° verdrehter Oberseite.
Antiwürfel Eigenschaften
Der gedrehte Würfel: Oberseite um 45° verdreht
Antiwürfel Struktur
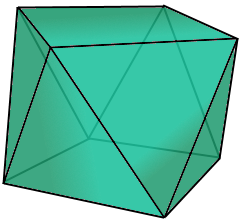
Der gedrehte Würfel mit 45° Verdrehung.
Verdrehung um 45°.
|
|
Was ist ein Antiwürfel?
Ein Antiwürfel ist ein faszinierender würfelartiger Körper:
- Definition: Würfel mit verdrehter Oberseite
- Verdrehung: Oberseite um 45° gedreht
- Flächen: 2 Quadrate + 8 Dreiecke
- Ecken: 10 Ecken insgesamt
- Kanten: 18 Kanten
- Symmetrie: Vierfache Drehsymmetrie
Geometrische Eigenschaften des Antiwürfels
Der Antiwürfel zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Grundfläche: Quadrat mit Seitenlänge a
- Deckfläche: Um 45° verdrehtes Quadrat
- Euler-Charakteristik: V - E + F = 10 - 18 + 10 = 2
- Verdrehungswinkel: Exakt 45°
Besondere Eigenschaften
- Chiralität: Nicht chiral (nicht spiegelbar)
- Seitenflächen: 8 kongruente Dreiecke
- Symmetrie: C4-Rotationssymmetrie
- Würfel-Verwandtschaft: Kubische Basis
Mathematische Beziehungen
Der Antiwürfel folgt eleganten mathematischen Gesetzen mit √2 und √3:
Volumen-Formel
Formel mit √2. Etwas weniger als ein Würfel.
Oberflächen-Formel
Formel mit √3. Mehr Oberfläche durch Verdrehung.
Anwendungen des Antiwürfels
Antiwürfel finden Anwendung in verschiedenen Bereichen:
Architektur & Design
- Moderne Gebäudekonstruktionen
- Gedrehte Turmstrukturen
- Innovative Raumkonzepte
- Skulpturale Elemente
Wissenschaft & Technik
- Kristallographische Modelle
- Mechanische Konstruktionen
- Optische Komponenten
- Strukturelle Analysen
Bildung & Lehre
- Geometrie-Unterricht
- Verdrehungs-Konzepte
- 3D-Visualisierung
- Mathematische Modelle
Kunst & Kreativität
- Skulpturale Werke
- Moderne Kunstobjekte
- Dekorative Designs
- Architektonische Kunst
Formeln zum Antiwürfel
Oberfläche (S)
Oberfläche mit √3-Faktor
Volumen (V)
Komplexe Volumenformel mit √2
Höhe (h)
Höhe reduziert durch Verdrehung
Verdrehungswinkel
Charakteristische 45° Verdrehung
Antiwürfel Parameter
Quadrat a×a
Um 45° gedreht
8 Dreiecke
≈ 0.84·a
Alle Eigenschaften entstehen durch die charakteristische 45° Verdrehung
Berechnungsbeispiel für einen Antiwürfel
Gegeben
Gesucht: Alle Eigenschaften des gedrehten Würfels
1. Oberflächen-Berechnung
Die Oberfläche beträgt 136.6 Flächeneinheiten
2. Volumen-Berechnung
Das Volumen beträgt 119.6 Volumeneinheiten
3. Höhen-Berechnung
Die Höhe beträgt 4.20 Längeneinheiten
4. Vergleich mit Würfel
Würfel: V = 125, S = 150
Antiwürfel: V = 119.6, S = 136.6
Weniger Volumen und Oberfläche durch Verdrehung
5. Der gedrehte Würfel
Der gedrehte Würfel mit perfekter 45° Verdrehung
Der Antiwürfel: Der gedrehte Würfel
Der Antiwürfel ist ein faszinierender geometrischer Körper, der die Eleganz der 45°-Verdrehung verkörpert. Durch die charakteristische Rotation der oberen Quadratfläche um exakt 45° entsteht eine einzigartige Struktur mit 8 dreieckigen Seitenflächen, die den Antiwürfel zu einem der interessantesten gedrehten Polyeder macht. Die mathematische Schönheit liegt in den eleganten Beziehungen mit √2 und √3, die alle geometrischen Eigenschaften miteinander verknüpfen und zeigen, wie eine einfache Verdrehung komplexe mathematische Strukturen erzeugen kann.
Die Geometrie der 45°-Verdrehung
Der Antiwürfel zeigt die Perfektion der 45°-Verdrehung:
- Verdrehungswinkel: Exakt 45° = π/4 Radiant
- Würfel-Verwandtschaft: Basiert auf kubischer Geometrie
- Flächenvielfalt: Kombination aus Quadraten und Dreiecken
- Symmetrie: Vierfache Rotationssymmetrie (C4)
- Höhenreduzierung: Geringere Höhe als der ursprüngliche Würfel
- Mathematische Eleganz: Formeln mit √2 und √3
- Eindeutigkeit: Spezifische 45°-Verdrehung
Mathematische Schönheit
Wurzel-Mathematik
Die Formeln des Antiwürfels sind elegant und verwenden √2 und √3, die fundamentalen Konstanten der Geometrie, um die durch die 45°-Verdrehung entstehenden Proportionen zu beschreiben.
Kubische Verwandtschaft
Trotz der Verdrehung behält der Antiwürfel seine kubische Verwandtschaft bei, was sich in den mathematischen Beziehungen und der strukturellen Symmetrie widerspiegelt.
Strukturelle Effizienz
Die 45°-Verdrehung erzeugt eine optimale Balance zwischen Stabilität und Materialeffizienz, was den Antiwürfel für technische Anwendungen interessant macht.
Ästhetische Vollendung
Die harmonische Kombination aus quadratischen Grundflächen und gleichmäßig angeordneten Dreiecken erzeugt eine einzigartige visuelle Dynamik.
Zusammenfassung
Der Antiwürfel verkörpert die perfekte Synthese aus kubischer Basis und innovativer Verdrehung. Seine 45°-Rotation, beschrieben durch elegante Formeln mit √2 und √3, macht ihn zu einem faszinierenden Studienobjekt für Mathematiker, Architekten und Designer. Als Brücke zwischen klassischer Würfelgeometrie und moderner Strukturinnovation zeigt der Antiwürfel, wie eine präzise geometrische Transformation zu völlig neuen Formen und Eigenschaften führen kann. Seine einzigartige Kombination aus mathematischer Eleganz und praktischer Anwendbarkeit macht ihn zu einem besonderen Beispiel für die Kraft der geometrischen Verdrehung.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder