Rhomboeder Rechner
Rechner und Formeln zur Berechnung eines Rhomboeders
Rhomboeder Rechner
Das Rhomboeder
Ein Rhomboeder ist ein Parallelepiped mit sechs kongruenten Rautenflächen.
Rhomboeder Eigenschaften
Der gescherte Würfel: Alle Flächen sind kongruente Rauten
Rhomboeder Struktur
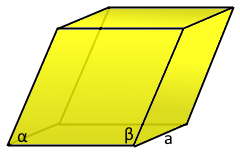
Der elegante gescherte Würfel mit Rautenflächen.
Spezialfall: Würfel bei α = 90°.
|
|
Was ist ein Rhomboeder?
Ein Rhomboeder ist ein faszinierender geometrischer Körper:
- Definition: Parallelepiped mit sechs kongruenten Rautenflächen
- Flächen: Alle sechs Flächen sind identische Rauten
- Kanten: Alle zwölf Kanten haben die gleiche Länge
- Winkel: Charakterisiert durch einen Kantenwinkel α
- Spezialfall: Würfel bei α = 90°
- Symmetrie: Hohe Rotationssymmetrie
Geometrische Eigenschaften des Rhomboeders
Das Rhomboeder zeigt faszinierende Eigenschaften gescherter Symmetrie:
Grundstruktur
- 6 Flächen: Alle sind kongruente Rauten
- 8 Ecken: Je drei Rauten treffen sich an jeder Ecke
- 12 Kanten: Alle haben dieselbe Länge a
- Parallelogramm-Struktur: Gegenüberliegende Flächen sind parallel
Besondere Eigenschaften
- Gescherte Würfel-Form: Würfel unter Scherung
- Kantenwinkel α: Bestimmt die Rautenform
- Supplementärwinkel β: β = 180° - α
- Hohe Symmetrie: Punktsymmetrie zum Mittelpunkt
Mathematische Beziehungen
Das Rhomboeder folgt komplexen trigonometrischen Gesetzen:
Volumen V
Komplexe Formel mit trigonometrischen Funktionen. Abhängig von Kantenlänge und Winkel.
Oberfläche S
Sechs gleiche Rautenflächen. Rautenfläche: a² sin α.
Anwendungen des Rhomboeders
Rhomboeder finden vielfältige Anwendung in Wissenschaft und Technik:
Kristallographie
- Calcit-Kristalle (Kalkspat)
- Dolomit-Mineralstrukturen
- Quarz-Varietäten in rhomboedrischer Form
- Hämatit und andere Eisenerze
Materialwissenschaft
- Kristallstruktur-Analyse
- Phasendiagramme und Gitterparameter
- Deformations- und Spannungsanalyse
- Anisotrope Materialien
Bildung & Forschung
- Geometrie-Unterricht und Raumvorstellung
- Trigonometrische Anwendungen
- Symmetrie-Studien und Gruppentheorie
- 3D-Visualisierung und CAD-Modellierung
Kunst & Design
- Skulpturen und Architekturelemente
- Schmuckdesign und Edelstein-Schliff
- Optische Instrumente und Prismen
- Dekorative Muster und Tessellationen
Formeln für das Rhomboeder
Volumen V
Komplexe trigonometrische Volumenformel
Oberfläche S
Sechs identische Rautenflächen
Supplementärwinkel β
Komplementärer Winkel in der Raute
Rautenfläche A_Raute
Fläche einer einzelnen Raute
Spezialfälle
\[V = a^3\]
\[S = 6a^2\]
Tetraeder-Winkel
Kollaps zu einer Ebene
Verschiedene Ausprägungen abhängig vom Kantenwinkel α
Geometrische Beziehungen
\[h = a\sqrt{1+2\cos \alpha}\]
\[d_1 = 2a\sin(\alpha/2)\]
\[d_2 = 2a\cos(\alpha/2)\]
\[A_{Grund} = a^2\sin \alpha\]
Zusätzliche geometrische Eigenschaften des Rhomboeders
Berechnungsbeispiel für ein Rhomboeder
Gegeben
Gesucht: Alle Eigenschaften des Rhomboeders
1. Supplementärwinkel berechnen
Der zweite Winkel in der Raute beträgt 120°
2. Oberfläche berechnen
Die Oberfläche beträgt etwa 519,6 Quadratzentimeter
3. Volumen berechnen
Das Volumen beträgt etwa 707,1 Kubikzentimeter
4. Rautendiagonalen
Die Diagonalen der Rautenflächen
5. Vergleich mit dem Würfel
Das 60°-Rhomboeder hat ein kleineres Volumen als der Würfel bei gleicher Kantenlänge
Das Rhomboeder: Geometrie der gescherten Symmetrie
Das Rhomboeder repräsentiert eine der elegantesten Formen der dreidimensionalen Geometrie - einen perfekt gescherten Würfel, bei dem alle sechs Flächen identische Rauten sind. Diese faszinierende Struktur verbindet die Regelmäßigkeit des Würfels mit der dynamischen Asymmetrie der Scherung und schafft dabei einen Körper von bemerkenswerer mathematischer Schönheit. Von Kristallstrukturen in der Natur bis zu architektonischen Meisterwerken verkörpert das Rhomboeder die perfekte Balance zwischen Ordnung und Bewegung.
Die Geometrie der gescherten Perfektion
Das Rhomboeder fasziniert durch seine einzigartige Struktur:
- Sechs Rautenflächen: Alle Flächen sind kongruente Rhomben mit Seitenlänge a
- Einheitliche Kantenlängen: Alle zwölf Kanten haben dieselbe Länge
- Charakteristischer Winkel α: Bestimmt die Form der Rauten
- Supplementärwinkel β: β = 180° - α vervollständigt die Rautenwinkel
- Parallelepiped-Struktur: Gegenüberliegende Flächen sind parallel
- Punktsymmetrie: Symmetrie bezüglich des Mittelpunkts
- Würfel als Spezialfall: Bei α = 90° entsteht der reguläre Würfel
Trigonometrische Eleganz
Volumenformel
Die Formel V = a³(1-cos α)√(1+2cos α) ist ein Meisterwerk der Trigonometrie. Sie zeigt, wie der Kantenwinkel das Volumen beeinflusst: bei α = 90° ergibt sich V = a³ (Würfel), das Maximum liegt bei α ≈ 109,47°.
Oberflächenberechnung
S = 6a² sin α ist eleganter: sechs identische Rauten mit Fläche a² sin α. Bei α = 90° wird sin α = 1, wodurch S = 6a² (Würfeloberfläche) entsteht.
Winkelabhängigkeit
Das Rhomboeder demonstriert perfekt, wie ein einziger Parameter (der Winkel α) die gesamte Geometrie bestimmt. Von flachen, fast zweidimensionalen Formen bis zu voluminösen, fast würfelartigen Strukturen.
Extremwerte
Bei α → 0° oder α → 180° kollabiert das Rhomboeder zu einer Ebene (V = 0). Das Volumen-Maximum liegt beim Tetraeder-Winkel α = arccos(-1/3) ≈ 109,47°.
Kristallographische Bedeutung
Das Rhomboeder ist fundamental für die Kristallographie:
Natürliche Mineralien
Calcit (CaCO₃) kristallisiert in perfekter rhomboedrischer Form mit α ≈ 78°. Diese Kristalle zeigen optische Doppelbrechung und wurden historisch für Polarisationsexperimente verwendet.
Dolomit-Strukturen
Dolomit [CaMg(CO₃)₂] bildet rhomboedrische Kristalle mit charakteristischen gebogenen Flächen. Diese Mineral-Familie zeigt die praktische Relevanz der Rhomboeder-Geometrie.
Gitterparameter
In der Kristallstruktur-Analyse werden Rhomboeder durch Gitterparameter a und α charakterisiert. Diese bestimmen alle physikalischen Eigenschaften wie Dichte, Härte und optische Eigenschaften.
Symmetriegruppen
Rhomboedrische Kristalle gehören zur trigonalen Kristallklasse mit der Raumgruppe R3m oder R3̄m, was ihre hohe Symmetrie mathematisch präzise beschreibt.
Historische und kulturelle Dimensionen
Die Bedeutung des Rhomboeders reicht weit über die Geometrie hinaus:
- Antike Mathematik: Frühe Studien zur Raumgeometrie und Symmetrie
- Optische Instrumente: Calcit-Prismen für Polarisations-Experimente
- Kristallographie-Entwicklung: Grundlage für moderne Strukturanalyse
- Architektonische Inspiration: Rhomboedrische Elemente in der Baukunst
- Schmuckdesign: Edelstein-Schliffe in rhomboedrischer Form
- Kunsthistorie: Isometrische Darstellungen und perspektivische Studien
- Moderne Materialforschung: Nanostrukturen und Metamaterialien
Mathematische Vertiefungen
Transformationsgeometrie
Das Rhomboeder entsteht durch Scherung eines Würfels entlang einer Raumdiagonale. Diese Transformation erhält Volumen und Parallelität, ändert aber Winkel und Abstände systematisch.
Vektorgeometrie
Mit drei Kantenvektoren der Länge a und Winkeln α lässt sich das Rhomboeder elegant beschreiben. Das Spatprodukt dieser Vektoren ergibt direkt das Volumen.
Gruppentheorie
Die Symmetriegruppe des Rhomboeders ist die Dihedergruppe D₃ mit 6 Elementen, was seine hohe, aber nicht kubische Symmetrie mathematisch präzise erfasst.
Optimierungsprobleme
Welcher Winkel α maximiert das Volumen bei gegebener Kantenlänge? Die Antwort α ≈ 109,47° (Tetraeder-Winkel) zeigt die Verbindung zu anderen platonischen Körpern.
Moderne Anwendungen und Technologie
Computergrafik
Rhomboeder eignen sich perfekt für isometrische Darstellungen in CAD-Software und Computerspielen. Ihre Symmetrie vereinfacht Rendering-Algorithmen erheblich.
Materialdesign
Metamaterialien mit rhomboedrischen Grundzellen zeigen einzigartige mechanische Eigenschaften: negative Poisson-Zahlen und programmierbare Steifigkeiten.
Architektonische Innovation
Moderne Architektur nutzt rhomboedrische Elemente für spektakuläre Fassaden und Strukturen, die Licht und Schatten auf faszinierende Weise modulieren.
Nanotechnologie
Nanopartikel in rhomboedrischer Form zeigen besondere optische und elektronische Eigenschaften, die für Photovoltaik und Quantentechnologie relevant sind.
Pädagogische Bedeutung
Raumvorstellung
Das Rhomboeder ist ideal für die Entwicklung räumlicher Vorstellungskraft. Seine Beziehung zum Würfel macht Transformationen und Symmetrien anschaulich begreifbar.
Trigonometrie
Die Volumen- und Oberflächenformeln demonstrieren perfekt die Anwendung trigonometrischer Funktionen in der Geometrie und verbinden abstrakte Mathematik mit konkreten Formen.
Interdisziplinarität
Rhomboeder verbinden Mathematik, Physik, Chemie und Kunst auf natürliche Weise und zeigen die Universalität geometrischer Prinzipien in der Natur.
Problemlösung
Die Analyse von Rhomboedern schult analytisches Denken und parametrische Betrachtungen - Fähigkeiten, die weit über die Geometrie hinaus relevant sind.
Zusammenfassung
Das Rhomboeder steht als Paradebeispiel für die Schönheit mathematischer Symmetrie und die Eleganz parametrischer Geometrie. Seine sechs identischen Rautenflächen verkörpern die perfekte Balance zwischen Regelmäßigkeit und Dynamik, zwischen der Stabilität des Würfels und der Flexibilität der Transformation. Von den Calcit-Kristallen in natürlichen Höhlen bis zu den futuristischen Fassaden moderner Architektur zeigt das Rhomboeder, wie ein einziger Parameter - der Kantenwinkel α - eine unendliche Vielfalt von Formen und Eigenschaften erzeugen kann. Als Bindeglied zwischen klassischer Geometrie und moderner Materialwissenschaft wird das Rhomboeder auch in Zukunft Mathematiker, Ingenieure und Künstler gleichermaßen inspirieren und neue Wege der Innovation eröffnen.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder