Parallelepiped Rechner
Rechner und Formeln zur Berechnung eines Parallelepiped
Parallelepiped Rechner
Das Parallelepiped
Ein Parallelepiped ist ein geometrischer Körper, der von 6 Parallelogrammen begrenzt wird.
Parallelepiped Eigenschaften
Der Parallelogramm-Körper: Spezielles Prisma mit parallelen Flächen
Parallelepiped Struktur
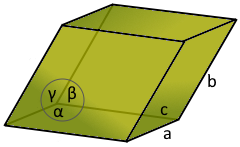
Der faszinierende schiefe Körper mit 6 Parallelogramm-Flächen.
Spezialfall eines Prismas.
|
|
Was ist ein Parallelepiped?
Ein Parallelepiped ist ein faszinierender geometrischer Körper:
- Definition: Körper mit 6 parallelogramm-förmigen Flächen
- Flächen: Je 2 gegenüberliegende sind kongruent und parallel
- Spezialfall: Des allgemeinen Prismas
- Ecken: 8 identische Ecken
- Kanten: 12 Kanten in drei Gruppen zu je 4
- Symmetrie: Zentral symmetrisch
Geometrische Eigenschaften des Parallelepipeds
Das Parallelepiped weist bemerkenswerte geometrische Eigenschaften auf:
Grundparameter
- Kantenlängen: Drei verschiedene Kantenlängen a, b, c
- Flächen: 6 parallelogramm-förmige Flächen
- Euler-Charakteristik: V - E + F = 8 - 12 + 6 = 2
- Spezialfälle: Quader, Rhomboeder, Würfel
Besondere Eigenschaften
- Prismatisch: Spezielles Prisma mit Parallelogramm-Basis
- Parallelogramm-Flächen: Alle Flächen sind Parallelogramme
- Zentral-symmetrisch: Punktsymmetrie zum Mittelpunkt
- Konvex: Alle Innenwinkel kleiner als 180°
Mathematische Beziehungen
Das Parallelepiped folgt komplexen mathematischen Gesetzmäßigkeiten mit trigonometrischen Funktionen:
Volumen-Formel
Komplexe Formel mit Kosinus-Produkten. Berücksichtigt alle drei Winkel zwischen den Kanten.
Oberflächen-Formel
Summe der sechs Parallelogramm-Flächen. Sinus-Funktionen für die Flächenberechnung.
Anwendungen des Parallelepipeds
Parallelepipede finden in verschiedenen Bereichen Anwendung:
Wissenschaft & Forschung
- Kristallographie und Mineralstruktur-Analyse
- Gitterzellen in der Festkörperphysik
- Mathematische Vektorrechnung
- Lineare Algebra und Determinanten
Technik & Design
- 3D-Modellierung und Computergrafik
- Architekturdesign und Bauplanung
- Verpackungsoptimierung
- Materialwissenschaft und Ingenieurwesen
Bildung & Lehre
- Geometrie-Unterricht und Demonstrationen
- Raumvorstellungs-Training
- Mathematische Anschauung
- Trigonometrie und Vektorrechnung
Kunst & Design
- Skulpturale Installationen
- Architektonische Elemente
- Dekorative Muster und Motive
- Moderne Kunstobjekte
Formeln für das Parallelepiped
Oberfläche A
Oberfläche als Summe der Parallelogramm-Flächen
Volumen V
Volumen mit komplexer Wurzel-Formel
Höhe h
Höhe des Parallelepipeds bezogen auf die Grundfläche
Spezialfälle
α = β = γ = 90°
V = a·b·c
a = b = c
α = β = γ
a = b = c
α = β = γ = 90°
Besondere Formen des Parallelepipeds
Berechnungsbeispiel für ein Parallelepiped
Gegeben
Gesucht: Alle Eigenschaften des schiefen Körpers
1. Kosinus-Werte berechnen
Konvertierung der Winkel in Kosinus-Werte
2. Sinus-Werte berechnen
Sinus-Werte für die Oberflächenberechnung
3. Volumen-Berechnung
Das Volumen beträgt etwa 160.3 Kubikeinheiten
4. Oberflächen-Berechnung
Die Oberfläche beträgt etwa 239.2 Quadrateinheiten
5. Höhen-Berechnung
Die Höhe beträgt etwa 4.45 Einheiten
6. Zusammenfassung der Ergebnisse
Der faszinierende schiefe Körper mit komplexer mathematischer Schönheit
Das Parallelepiped: Der Geheimnisvolle Schiefe Körper
Das Parallelepiped ist einer der faszinierendsten und zugleich praktischsten geometrischen Körper. Mit seinen 6 parallelogramm-förmigen Flächen verkörpert es eine einzigartige Verbindung zwischen mathematischer Komplexität und praktischer Anwendbarkeit. Als spezieller Fall eines Prismas mit parallelogramm-förmiger Grundfläche repräsentiert es die Grundlagen der Vektorgeometrie und linearen Algebra, wo jede seiner Kanten durch Vektoren dargestellt werden kann und das Volumen durch das Spatprodukt dreier Vektoren berechnet wird.
Die Geometrie der Parallelogramm-Flächen
Das Parallelepiped fasziniert durch seine einzigartigen Flächeneigenschaften:
- 6 Parallelogramm-Flächen: Alle Flächen sind Parallelogramme mit parallelen Gegenseiten
- Drei Kantenlängen: Jede der drei Raumrichtungen hat eine charakteristische Länge (a, b, c)
- Charakteristische Winkel: Drei Winkel α, β, γ zwischen den Kanten bestimmen die Form
- Parallelität: Gegenüberliegende Flächen sind parallel und kongruent
- Zentrale Symmetrie: Alle Eigenschaften sind bezüglich des Mittelpunkts symmetrisch
- Perfekte Anordnung: Die 6 Parallelogramme fügen sich zu einem vollständig symmetrischen Körper zusammen
- Prismatisches Prinzip: Jede Parallelogramm-Fläche kann als Grundfläche dienen
Spezialfälle und geometrische Familie
Quader (Rechteckiges Parallelepiped)
Wenn alle Winkel 90° betragen (α = β = γ = 90°), entsteht der Quader - die rechteckige Form des Parallelepipeds mit besonders einfachen Berechnungsformeln.
Rhomboeder
Wenn alle Kantenlängen gleich sind (a = b = c) und alle Winkel gleich (α = β = γ), entsteht das Rhomboeder - ein "schiefer Würfel" mit besonderen Symmetrieeigenschaften.
Würfel
Die Kombination beider Spezialfälle (a = b = c und α = β = γ = 90°) ergibt den Würfel - den perfektesten Spezialfall des Parallelepipeds.
Allgemeine Form
Das allgemeine Parallelepiped mit beliebigen Kantenlängen und Winkeln zeigt die vollständige mathematische Komplexität dieser Körperklasse.
Trigonometrie und Vektorrechnung
Das Parallelepiped ist durchdrungen von trigonometrischen Beziehungen:
Winkel-Beziehungen
Die drei Winkel α, β, γ zwischen den Kanten bestimmen vollständig die Form des Parallelepipeds. Diese Winkel erscheinen in Kosinus-Form in der Volumenformel und in Sinus-Form in der Oberflächenformel.
Vektor-Darstellung
Jedes Parallelepiped kann durch drei Vektoren dargestellt werden, wodurch sich elegante Berechnungsmethoden mit dem Spatprodukt ergeben: V = |a⃗ · (b⃗ × c⃗)|.
Determinanten-Berechnung
Das Volumen entspricht dem Betrag der Determinante der Matrix, die aus den drei Kantenvektoren gebildet wird - eine zentrale Verbindung zur linearen Algebra.
Komplexe Wurzel-Formeln
Die Volumenformel enthält eine komplexe Wurzel mit Kosinus-Produkten, die die dreidimensionale Geometrie des schiefen Körpers widerspiegelt.
Wissenschaftliche und kulturelle Bedeutung
Das Parallelepiped findet Anwendungen in verschiedensten Bereichen:
- Kristallographie: Grundform für Kristallgitter und Einheitszellen
- Festkörperphysik: Modell für Gitterstrukturen und Brillouin-Zonen
- Mathematische Forschung: Untersuchungsobjekt für Volumen-Optimierung und Packungsprobleme
- Architektur: Basis für schiefe Gebäude und moderne Bauwerke
- Bildung: Demonstration von Vektorrechnung und linearer Algebra
- Computergrafik: Grundform für 3D-Transformationen und Rendering
- Materialwissenschaft: Modell für Verformung und Scherung
Konstruktion und mathematische Herausforderungen
Konstruktions-Schwierigkeiten
Die Herstellung eines perfekten Parallelepipeds erfordert höchste Präzision bei der Einhaltung der Winkel und Parallelitäten. Bereits kleinste Abweichungen können die geometrischen Eigenschaften zerstören.
Mathematische Komplexität
Die Berechnungen erfordern trigonometrische Funktionen und Wurzelausdrücke, was diesen Körper zu einem der anspruchsvollsten in der Elementargeometrie macht.
Moderne Technologie
Erst mit moderner CAD-Software und Präzisionsfertigung ist es möglich geworden, physische Modelle mit der erforderlichen Genauigkeit zu erstellen.
Qualitätskontrolle
Die Überprüfung der geometrischen Korrektheit erfordert hochpräzise Messmethoden und rechnergestützte Analysesysteme.
Philosophische und ästhetische Dimensionen
Harmonie der Gegensätze
Das Parallelepiped verkörpert die Harmonie zwischen Ordnung (parallele Flächen) und Freiheit (beliebige Winkel), was es zu einem philosophischen Symbol macht.
Natürliche Schönheit
Die Proportionen und Winkel können so gewählt werden, dass natürlich wirkende und ästhetisch ansprechende Formen entstehen.
Bildungswert
Als Demonstrationsobjekt für Vektorrechnung, Trigonometrie und räumliche Geometrie bietet es unvergleichliche Möglichkeiten für Mathematikunderricht.
Kulturelle Symbolik
In verschiedenen Kulturen werden schiefe Strukturen mit Dynamik, Bewegung und progressivem Denken assoziiert.
Zusammenfassung
Das Parallelepiped steht als einer der vielseitigsten und mathematisch anspruchsvollsten geometrischen Körper da. Seine 6 parallelogramm-förmigen Flächen, durchdrungen von trigonometrischen Beziehungen und in perfekter räumlicher Anordnung, machen es zu einem Meisterwerk der Geometrie. Von seiner Entdeckung als Verallgemeinerung des Quaders bis zu seinen modernen Anwendungen in Wissenschaft und Technik zeigt es, wie mathematische Abstraktion und praktische Anwendbarkeit eine untrennbare Einheit bilden können. Als Brücke zwischen der elementaren Geometrie der Antike und den modernen Herausforderungen der Vektorrechnung und linearen Algebra bleibt es ein faszinierendes Untersuchungsobjekt für Forscher, Ingenieure und alle, die von der Kraft der Mathematik inspiriert sind, perfekte dreidimensionale Formen zu schaffen.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder