Prismatoid Rechner
Rechner und Formeln zur Berechnung eines Prismatoid
Prismatoid Rechner
Das Prismatoid
Ein Prismatoid ist ein geometrischer Körper mit parallelen Polygonen als Grund- und Deckfläche.
Prismatoid Eigenschaften
Der vielseitige Körper: Parallele Polygone als Basis und Deckfläche
Prismatoid Struktur
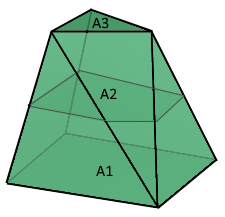
Der vielseitige geometrische Körper mit parallelen Polygonflächen.
Unterschied zum Prisma: verschiedene Basis- und Deckflächen möglich.
|
|
Was ist ein Prismatoid?
Ein Prismatoid ist ein vielseitiger geometrischer Körper:
- Definition: Körper mit zwei parallelen Polygonen als Grund- und Deckfläche
- Seitenflächen: Dreiecke, Trapeze oder Parallelogramme
- Flexibilität: Basis und Deckfläche können unterschiedlich sein
- Unterschied zum Prisma: Basis und Deckfläche müssen nicht kongruent sein
- Eckenzahl: Verschiedene Eckenzahlen bei Basis und Deckfläche möglich
- Berechnung: Simpsonsche Regel für Volumenberechnung
Geometrische Eigenschaften des Prismatoids
Das Prismatoid zeigt bemerkenswerte geometrische Vielseitigkeit:
Grundstruktur
- Zwei parallele Flächen: Grundfläche A₁ und Deckfläche A₃
- Mittlere Querschnittfläche: A₂ in halber Höhe
- Höhe h: Abstand zwischen den parallelen Flächen
- Seitenflächen: Verbinden die Kanten der parallelen Flächen
Besondere Eigenschaften
- Flexible Geometrie: Basis und Deckfläche können beliebige Polygone sein
- Verschiedene Eckenzahlen: Dreiecks-Basis mit Sechseck-Deckfläche möglich
- Prisma als Spezialfall: Wenn Basis und Deckfläche kongruent sind
- Pyramide als Spezialfall: Wenn eine Fläche ein Punkt ist
Mathematische Beziehungen
Das Prismatoid folgt der eleganten Simpsonschen Regel:
Volumenformel
Simpsonsche Regel: gewichteter Durchschnitt der Querschnittflächen. Die mittlere Fläche wird vierfach gewichtet.
Höhenformel
Umformung der Volumenformel zur Höhenberechnung. Praktisch bei bekanntem Volumen.
Anwendungen des Prismatoids
Prismatoide finden Anwendung in vielen praktischen Bereichen:
Ingenieurwesen
- Erdvolumen-Berechnung beim Straßenbau
- Damm- und Deichbau Kalkulationen
- Volumenbestimmung bei Aushubarbeiten
- Betonvolumen für Fundamente
Architektur & Bauwesen
- Treppenhaus-Volumenberechnung
- Dachkonstruktionen mit variablen Querschnitten
- Materialbedarfs-Kalkulationen
- Raumvolumen komplexer Gebäudeteile
Produktion & Design
- Behälter und Tanks mit konischen Formen
- Gussformen für die Metallverarbeitung
- Produktdesign mit variablen Querschnitten
- 3D-Druck Volumenoptimierung
Wissenschaft & Forschung
- Numerische Integration in der Mathematik
- Volumenbestimmung geologischer Formationen
- Kristallographie und Materialwissenschaft
- Bildungswesen und Geometrie-Unterricht
Formeln für das Prismatoid
Volumen V
Simpsonsche Regel mit gewichteten Querschnittflächen
Höhe h
Umstellung der Volumenformel nach der Höhe
Flächenbezeichnungen
Untere Polygonfläche
Mittlere Fläche bei h/2
Obere Polygonfläche
Die drei charakteristischen Querschnittflächen des Prismatoids
Simpsonsche Regel
Gewichtung der Flächen:
Grundfläche A₁: Gewicht 1
Mittelfläche A₂: Gewicht 4
Deckfläche A₃: Gewicht 1
Die mittlere Fläche wird vierfach gewichtet, da sie den größten Einfluss auf das Volumen hat.
Berechnungsbeispiel für ein Prismatoid
Gegeben
Gesucht: Volumen des Prismatoids
1. Simpsonsche Regel anwenden
Einsetzen der gegebenen Werte in die Formel
2. Klammer berechnen
Berechnung der gewichteten Summe der Flächen
3. Volumen berechnen
Das Volumen beträgt etwa 123.33 Kubikeinheiten
4. Vergleich mit anderen Methoden
\[\frac{5+8}{2} \cdot 20 = 130\]
Unterschied: 6.67 m³
Die Simpsonsche Regel ist präziser als der einfache Durchschnitt
5. Ergebnis und Interpretation
Das Prismatoid mit variablen Querschnittflächen zeigt die Eleganz der Simpsonschen Regel
Das Prismatoid: Der vielseitige geometrische Körper
Das Prismatoid ist einer der vielseitigsten und praktisch relevantesten geometrischen Körper in der angewandten Mathematik. Mit seiner charakteristischen Struktur aus zwei parallelen Polygonflächen als Basis und Deckfläche sowie den verbindenden Seitenflächen verkörpert es eine perfekte Balance zwischen geometrischer Einfachheit und praktischer Anwendbarkeit. Die elegante Volumenberechnung durch die Simpsonsche Regel macht es zu einem unverzichtbaren Werkzeug in Ingenieurwesen, Architektur und vielen anderen technischen Disziplinen.
Die Geometrie des Prismatoids
Das Prismatoid fasziniert durch seine strukturelle Flexibilität:
- Parallele Polygonflächen: Grundfläche A₁ und Deckfläche A₃ können beliebige Polygone sein
- Variable Eckenzahlen: Dreiecks-Basis kann mit Sechseck-Deckfläche kombiniert werden
- Mittlere Querschnittfläche: A₂ in halber Höhe bestimmt die Volumenberechnung entscheidend mit
- Seitenflächen: Entstehen als Dreiecke, Trapeze oder Parallelogramme je nach Eckenzahl
- Höhe h: Konstanter Abstand zwischen den parallelen Flächen
- Flexible Geometrie: Von einfachen bis zu hochkomplexen Formen möglich
- Spezialfälle: Prisma (kongruente Flächen) und Pyramide (eine Fläche als Punkt)
Die Simpsonsche Regel
Mathematische Eleganz
Die Simpsonsche Regel V = h/6 · (A₁ + 4A₂ + A₃) ist ein Meisterwerk der numerischen Integration. Sie gewichtet die mittlere Fläche vierfach, da diese den größten Einfluss auf das tatsächliche Volumen hat.
Präzision
Im Vergleich zur einfachen Durchschnittsbildung liefert die Simpsonsche Regel erheblich präzisere Ergebnisse, besonders bei stark variierenden Querschnittflächen.
Praktische Anwendung
Die Regel ermöglicht es, komplexe dreidimensionale Formen mit nur drei Flächenmessungen exakt zu berechnen - ein enormer Vorteil in der Praxis.
Numerische Integration
Das Prismatoid demonstriert perfekt, wie numerische Methoden geometrische Probleme elegant lösen können, ohne komplexe Integralrechnungen durchführen zu müssen.
Praktische Bedeutung in Technik und Wissenschaft
Das Prismatoid ist weit mehr als nur ein theoretisches Konzept:
Ingenieurwesen
Von der Erdvolumen-Berechnung beim Straßenbau bis zur Dimensionierung von Dämmen und Deichen - das Prismatoid ist unverzichtbar für Volumenkalkulationen bei unregelmäßigen Geometrien.
Architektur
Moderne Architektur mit ihren komplexen, organischen Formen nutzt die Prismatoid-Geometrie für Volumenberechnungen von Treppen, Rampen und freitragenden Konstruktionen.
Produktion
In der industriellen Fertigung ermöglicht das Prismatoid die präzise Berechnung von Materialvolumen für Gussformen, Behälter und komplexe Bauteile.
Wissenschaft
Von der Geologie bis zur Kristallographie dient das Prismatoid als mathematisches Modell für natürliche und künstliche Strukturen mit variierenden Querschnitten.
Historische Entwicklung und moderne Relevanz
Die Entwicklung des Prismatoid-Konzepts spiegelt die Evolution der angewandten Mathematik wider:
- Antike Grundlagen: Bereits die alten Ägypter berechneten Pyramidenvolumen mit ähnlichen Prinzipien
- Renaissance: Systematische Entwicklung von Volumenformeln für komplexe Körper
- Simpson (1710-1761): Formalisierung der nach ihm benannten Regel für numerische Integration
- Industrialisierung: Praktische Anwendung bei großen Bauprojekten und Erdarbeiten
- Computer-Zeitalter: Integration in CAD-Software und automatisierte Berechnungssysteme
- Moderne Anwendungen: 3D-Druck, digitale Architektur und parametrisches Design
- Zukunftsperspektiven: KI-gestützte Optimierung und adaptive Geometrien
Mathematische Verallgemeinerungen
Erweiterte Formen
Das Prismatoid-Konzept lässt sich auf beliebig viele Zwischenflächen erweitern, was zu noch präziseren Volumenberechnungen bei komplexen Geometrien führt.
Numerische Methoden
Moderne finite-Elemente-Verfahren basieren auf Prismatoid-ähnlichen Grundelementen, wodurch komplexeste dreidimensionale Strukturen berechenbar werden.
Computergrafik
In der 3D-Computergrafik dienen Prismatoid-Segmente als Basis für die Darstellung organischer Formen und die Volumenberechnung in Rendering-Algorithmen.
Optimierung
Das Prismatoid ermöglicht Materialoptimierung durch präzise Volumenvorhersagen bei der Entwicklung ressourcenschonender Konstruktionen.
Didaktische und kulturelle Bedeutung
Bildungswert
Das Prismatoid ist ein perfektes Lehrobjekt für die Verbindung zwischen theoretischer Geometrie und praktischer Anwendung, da es komplexe mathematische Konzepte greifbar macht.
Problemlösungsansätze
Die Simpsonsche Regel demonstriert exemplarisch, wie elegante mathematische Methoden komplexe technische Probleme lösbar machen.
Interdisziplinarität
Das Prismatoid verbindet Geometrie, Analysis, Ingenieurwissenschaften und Informatik und zeigt die Universalität mathematischer Konzepte.
Innovation
Moderne Innovationen in Architektur, Design und Technik nutzen Prismatoid-Prinzipien für die Entwicklung neuartiger, effizienter Strukturen.
Zusammenfassung
Das Prismatoid steht als Paradebeispiel für die praktische Eleganz der Mathematik da. Seine Fähigkeit, komplexe dreidimensionale Formen mit einer einfachen, präzisen Formel zu beschreiben, macht es zu einem unverzichtbaren Werkzeug in Technik und Wissenschaft. Von der antiken Geometrie bis zur modernen Computergrafik zeigt das Prismatoid, wie zeitlose mathematische Prinzipien immer neue Anwendungen finden. Die Simpsonsche Regel, verkörpert in der Prismatoid-Berechnung, demonstriert die Kraft der numerischen Mathematik, reale Probleme mit beeindruckender Genauigkeit und Effizienz zu lösen. Als Brücke zwischen theoretischer Geometrie und praktischer Anwendung wird das Prismatoid auch in Zukunft eine zentrale Rolle in der Entwicklung innovativer technischer Lösungen spielen.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder