Sterntetraeder Rechner
Rechner und Formeln zur Berechnung des Volumens und der Oberfläche eines Sterntetraeder
Sterntetraeder Rechner
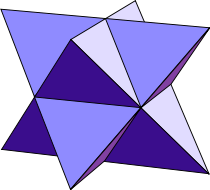
Das Sterntetraeder
Ein Sterntetraeder ist ein achtstrahliger Stern, bekannt als Stella Octangula und Keplerstern.
|
|
Was ist ein Sterntetraeder?
Ein Sterntetraeder ist ein faszinierender achtstrahliger Stern:
- Definition: Vielflächiger Körper aus zwei punktsymmetrischen Tetraedern
- Namen: Auch bekannt als Stella Octangula und Keplerstern
- Form: Achtstrahliger Stern mit tetraedrischen Spitzen
- Flächen: 8 gleichseitige Dreiecksflächen
- Eigenschaften: Gehört zu den nicht-konvexen Deltaedern
- Symmetrie: Hohe tetraedrische Symmetrie
Geometrische Eigenschaften des Sterntetraeders
Das Sterntetraeder zeigt bemerkenswerte geometrische Eigenschaften:
Grundstruktur
- Entstehung: Verschmelzung zweier punktsymmetrischer Tetraeder
- Achtstrahlig: Acht tetraedrische Spitzen strahlen aus dem Zentrum
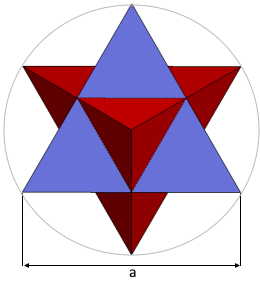
- Kantenlänge b: Innere Kantenlänge b = a/2
- Symmetrie: Tetraedrische Punktgruppe
Besondere Eigenschaften
- Nicht-konvex: Gehört zu den nicht-konvexen Deltaedern
- Stella Octangula: Historischer Name von Kepler
- Doppeltetraeder: Zwei ineinander verschränkte Tetraeder
- Achteckiger Stern: Dreidimensionale Sternform
Mathematische Beziehungen
Das Sterntetraeder folgt eleganten mathematischen Gesetzen:
Volumenformel
Elegante Formel mit Wurzel aus 2. Einfache Beziehung zur Kantenlänge.
Oberflächenformel
Oberfläche mit Wurzel aus 3. Acht gleichseitige Dreiecke.
Anwendungen des Sterntetraeders
Sterntetraeder finden Anwendung in verschiedenen Bereichen:
Wissenschaft & Forschung
- Kristallographie und Mineralstruktur-Analyse
- Molekulargeometrie komplexer Verbindungen
- Astronomische Sternsymmetrie-Studien
- Mathematische Topologie und Geometrie
Technik & Design
- 3D-Modellierung und Computergrafik
- Architektonische Sternstrukturen
- Ingenieurskonstruktionen mit Symmetrie
- Mathematische Visualisierungssoftware
Bildung & Lehre
- Geometrie-Unterricht und Demonstrationen
- Polyeder-Studien und Sternkörper
- Symmetrie-Konzepte in der Mathematik
- Keplersche Sterne und historische Geometrie
Kunst & Gestaltung
- Skulpturale Installationen und Sternformen
- Dekorative Muster und Ornamente
- Architektonische Gestaltungselemente
- Mathematische Kunst und Symmetriedesign
Formeln für das Sterntetraeder
Kantenlänge b
Innere Kantenlänge der Tetraeder
Volumen V
Volumen mit Wurzel aus 2
Oberfläche S
Oberfläche mit Wurzel aus 3
Umkreisradius ru
Umkreisradius mit Wurzel aus 6
Kantenradius rk
Kantenradius mit Wurzel aus 2
Innenradius ri
Innenradius mit Wurzel aus 6
Zusammenhänge der Radien
ru = √6 · rk
rk = √3 · ri
ru : rk : ri = √6 : √2 : 1
Die charakteristischen Verhältnisse der Sterntetraeder-Radien
Berechnungsbeispiel für ein Sterntetraeder
Gegeben
Gesucht: Alle Eigenschaften des achtstrahliges Sterns
1. Kantenlänge b
Die innere Kantenlänge beträgt 2 Einheiten
2. Volumenberechnung
Das Volumen beträgt etwa 11.31 Kubikeinheiten
3. Oberflächenberechnung
Die Oberfläche beträgt etwa 41.57 Flächeneinheiten
4. Umkreisradius
Der Umkreisradius beträgt etwa 2.45 Einheiten
5. Kantenradius
Der Kantenradius beträgt etwa 1.41 Einheiten
6. Innenradius
Der Innenradius beträgt etwa 0.82 Einheiten
7. Zusammenfassung aller Eigenschaften
Der faszinierende achtstrahlige Stern mit eleganter mathematischer Struktur
Das Sterntetraeder: Der geheimnisvolle achtstrahlige Stern
Das Sterntetraeder, auch bekannt als Stella Octangula und Keplerstern, ist eines der faszinierendsten und historisch bedeutsamsten geometrischen Objekte. Dieser achtstrahlige Stern entsteht durch die perfekte Verschmelzung zweier punktsymmetrischer Tetraeder und verkörpert eine einzigartige Verbindung zwischen mathematischer Eleganz und dreidimensionaler Schönheit. Als nicht-konvexes Deltaeder gehört es zu den besonderen Polyedern, die sowohl in der Mathematik als auch in der Kunst und Philosophie eine wichtige Rolle spielen.
Die Struktur des Sterntetraeders
Das Sterntetraeder fasziniert durch seine einzigartige geometrische Konstruktion:
- Doppeltetraeder: Zwei identische Tetraeder werden so ineinander verschränkt, dass sie einen achtstrahliger Stern bilden
- Punktsymmetrie: Die beiden Tetraeder sind punktsymmetrisch zueinander angeordnet
- Acht Spitzen: Jede der acht Ecken der beiden Tetraeder wird zu einer Sternspitze
- Kantenverhältnis: Die innere Kantenlänge b ist genau die Hälfte der äußeren Kantenlänge a
- Nicht-konvex: Die einspringenden Kanten machen es zu einem nicht-konvexen Polyeder
- Deltaeder: Alle Flächen sind kongruente gleichseitige Dreiecke
- Symmetrieachsen: Besitzt vier dreizählige Symmetrieachsen durch gegenüberliegende Sternspitzen
Historische Bedeutung und Namen
Keplersche Tradition
Johannes Kepler (1571-1630) entdeckte und benannte diesen Körper als "Stella Octangula" (achteckiger Stern). In seinem Werk "Harmonices Mundi" (1619) beschrieb er die harmonischen Proportionen dieses geometrischen Wunders.
Mathematische Namen
Als "Sterntetraeder" verdeutlicht der Name die Entstehung aus Tetraedern. "Stella Octangula" betont die achteckige Sternform, während "Keplerstern" den historischen Entdecker ehrt.
Deltaeder-Familie
Als eines der acht nicht-konvexen Deltaeder (Polyeder mit ausschließlich dreieckigen Flächen) steht es in einer besonderen mathematischen Tradition neben Tetraeder, Oktaeder und Ikosaeder.
Symmetriegruppe
Mit der tetraedrischen Symmetriegruppe Td besitzt es 24 Symmetrieoperationen, was es zu einem hochsymmetrischen Objekt macht.
Die Eleganz der mathematischen Formeln
Das Sterntetraeder zeichnet sich durch besonders elegante mathematische Beziehungen aus:
Einfache Proportionen
Die Kantenlänge der inneren Tetraeder ist genau die Hälfte der äußeren Kantenlänge: b = a/2. Diese einfache Beziehung macht Berechnungen besonders elegant.
Wurzel-Beziehungen
Alle wichtigen Größen lassen sich durch die Grundwurzeln √2, √3 und √6 ausdrücken, was die tiefe mathematische Harmonie des Körpers zeigt.
Radius-Verhältnisse
Die drei charakteristischen Radien stehen im harmonischen Verhältnis √6 : √2 : 1, was geometrisch bedeutsame Proportionen schafft.
Volumen-Formel
Die Volumenformel V = (a³·√2)/8 zeigt, wie aus der kubischen Kantenlänge durch √2 das Volumen des achtstrahliges Sterns entsteht.
Wissenschaftliche und kulturelle Bedeutung
Das Sterntetraeder findet Anwendung in vielen Bereichen:
- Kristallographie: Modell für bestimmte Kristallstrukturen mit tetraedrischer Symmetrie
- Molekularchemie: Template für sternförmige Molekülstrukturen und Koordinationsverbindungen
- Astronomie: Symbol für Sternsymmetrien und kosmische Harmonie
- Architektur: Inspiration für sternförmige Bauwerke und Ornamente
- Kunst: Symbol für Perfektion, Harmonie und mathematische Schönheit
- Philosophie: Metapher für die Vereinigung von Gegensätzen in höherer Ordnung
- Bildung: Lehrobjekt für Symmetrie, Polyeder und dreidimensionale Geometrie
Konstruktion und praktische Herausforderungen
Geometrische Konstruktion
Die Konstruktion erfordert präzise Positionierung zweier Tetraeder. Jedes Tetraeder muss so rotiert werden, dass seine Ecken exakt zwischen die Flächen des anderen zeigen.
Materielle Herstellung
Die Herstellung physischer Modelle ist anspruchsvoll, da die acht Spitzen exakt ausgerichtet sein müssen. Moderne 3D-Drucktechnologie ermöglicht präzise Realisierungen.
Mathematische Verifikation
Die Überprüfung der korrekten Geometrie erfordert präzise Messungen aller Winkel und Abstände. Schon kleine Abweichungen können die Symmetrie zerstören.
Visualisierung
Die komplexe dreidimensionale Struktur macht das Sterntetraeder zu einer Herausforderung für die graphische Darstellung und räumliche Vorstellung.
Philosophische und ästhetische Dimensionen
Symbolik der Vereinigung
Das Sterntetraeder symbolisiert die perfekte Vereinigung zweier identischer, aber entgegengesetzter Elemente zu einer höheren Einheit - ein kraftvolles Bild für Harmonie und Balance.
Mathematische Schönheit
Die eleganten Formeln und harmonischen Proportionen machen es zu einem Paradebeispiel für die Schönheit der Mathematik in der Geometrie.
Pädagogischer Wert
Als Demonstrationsobjekt für Symmetrie, Polyedertheorie und dreidimensionales Denken ist es unschätzbar wertvoll für den Mathematikunterricht.
Kulturelle Resonanz
Die Sternform spricht universelle ästhetische Empfindungen an und verbindet mathematische Exaktheit mit künstlerischer Ausdruckskraft.
Das Sterntetraeder in der modernen Mathematik
Heute spielt das Sterntetraeder wichtige Rollen in verschiedenen mathematischen Disziplinen:
Polyedertheorie
Als nicht-konvexes Deltaeder ist es ein wichtiges Studienobjekt für die Klassifikation von Polyedern und die Untersuchung von Symmetrieeigenschaften.
Gruppentheorie
Seine tetraedrische Symmetriegruppe Td macht es zu einem idealen Beispiel für die Anwendung der Gruppentheorie in der Geometrie.
Topologie
Die nicht-konvexe Struktur und die komplexe Oberflächentopologie machen es interessant für topologische Studien und Algorithmenentwicklung.
Computergrafik
Als Benchmark für Rendering-Algorithmen und 3D-Modellierungssoftware testet es die Grenzen moderner Computergrafik-Systeme.
Zusammenfassung
Das Sterntetraeder steht als einer der elegantesten und historisch bedeutsamsten geometrischen Körper da. Von Keplers Entdeckung als Stella Octangula bis zu modernen Anwendungen in Wissenschaft und Kunst verkörpert es die perfekte Verbindung von mathematischer Exaktheit und ästhetischer Schönheit. Seine einfachen, aber kraftvollen Formeln, die harmonischen Proportionen und die symbolische Bedeutung als Vereinigung von Gegensätzen machen es zu einem zeitlosen Meisterwerk der Geometrie. Als Bindeglied zwischen antiker mathematischer Tradition und moderner dreidimensionaler Gestaltung inspiriert es weiterhin Mathematiker, Künstler und alle, die von der Macht der Symmetrie und der Schönheit geometrischer Formen fasziniert sind.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder