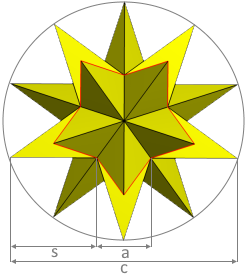
Ikosaederstern berechnen
Rechner und Formeln zur Berechnung eines Ikosaederstern
Diese Funktion berechnet verschiedene Parameter eines Ikosaederstern.
Wählen Sie die Eigenschaft aus die Ihnen bekannt ist und geben Sie deren Wert ein. Anschließend klicken Sie auf 'Berechnen'.
|
Formeln zum Ikosaederstern
Kantenlänge (\(\small{s}\))
\(\displaystyle s = \frac{a}{2} \cdot (1 + \sqrt{5})\) \(\displaystyle \;\;\; ≈ a \cdot 1.618\)
Sehnenlänge (\(\small{c}\))
\(\displaystyle c = a \cdot (2 + \sqrt{5})\) \(\displaystyle \;\;\; ≈ a \cdot 4.236\)
Volumen (\(\small{V}\))
\(\displaystyle V=\frac{5}{4} \cdot a^3 \cdot (3 + \sqrt{5})\) \(\displaystyle \;\;\; ≈ a^3 \cdot 6.545\)
Oberfläche (\(\small{S}\))
\(\displaystyle S= 15\cdot a^2 \cdot \sqrt{5 + 2 \cdot \sqrt{5}}\) \(\displaystyle \;\;\; ≈ a^2 \cdot 46.165\)
Umkreisradius (\(\small{r}\))
\(\displaystyle r=\frac{a}{4} \cdot \sqrt{3} \cdot (3 + \sqrt{5})\) \(\displaystyle \;\;\; ≈ a \cdot 2.267\)
Höhe (\(\small{h}\))
\(\displaystyle h = \frac{a}{6} \cdot \sqrt{3} \cdot (3 + \sqrt{5})\) \(\displaystyle \;\;\; ≈ a \cdot 1.512 \)
Quader
•
Quadratische Säule
•
Antiprisma
•
Sechseckprisma
•
Dreiecksprisma
•
Regelmäßiges Prisma
•
Schiefes Prisma
•
Rampe
•
Antiwürfel
•
Keil
•
Gerader Keil
•
Rhomboeder
•
Parallelepiped
•
Tetraeder, allgemeines
•
Pentagonales Trapezoeder
•
Tetragonales Trapezoeder
•
Prismatoid
•
Sterntetraeder
•
Dodekaederstern
•
Ikosaederstern
•
Großes Dodekaeder
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder
|
|