Oktaeder Rechner
Onlinerechner und Formeln zur Berechnung eines Oktaeders
Oktaeder Rechner
Das Oktaeder
Das Oktaeder ist ein platonischer Körper mit 8 gleichseitigen Dreiecken und √2-Beziehungen.
Platonischer Körper Eigenschaften
Der Doppel-Pyramiden-Körper: 8 gleichseitige Dreiecke mit √2-Proportionen
Oktaeder Struktur
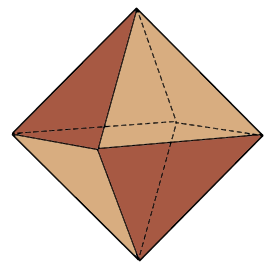
Der platonische Körper mit 8 Dreiecken.
Dual zum Würfel (Hexaeder).
|
|
Was ist ein Oktaeder?
Das Oktaeder ist einer der fünf platonischen Körper:
- Definition: Körper mit 8 gleichseitigen Dreiecken
- Platonischer Körper: Einer der fünf regulären Polyeder
- Flächen: 8 kongruente gleichseitige Dreiecke
- Ecken: 6 Ecken insgesamt
- Kanten: 12 Kanten
- √2-Beziehungen: Basis aller Proportionen
Geometrische Eigenschaften des Oktaeders
Das Oktaeder zeigt die Eleganz der doppelten Pyramiden-Struktur:
Grundparameter
- Flächen: 8 gleichseitige Dreiecke
- Ecken: 6 Ecken
- Kanten: 12 Kanten (alle gleich lang)
- Euler-Charakteristik: V - E + F = 6 - 12 + 8 = 2
Besondere Eigenschaften
- Deltaeder: Alle Flächen sind Dreiecke
- Würfel-Dual: Dual zum Würfel (Hexaeder)
- Platonisch: Einer der fünf regulären Polyeder
- Doppel-Pyramide: Zwei vierseitige Pyramiden
Mathematische Beziehungen
Das Oktaeder folgt den eleganten √2-Gesetzen:
Volumen-Formel
Enthält die Quadratwurzel von 2. Elegant und einfach.
Oberflächen-Formel
8 gleichseitige Dreiecke. Einfache √3 Beziehung.
Anwendungen des Oktaeders
Oktaeder finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Strukturelle Verstrebungen
- Raumfachwerke
- Dekorative Elemente
- Moderne Architektur
Wissenschaft & Technik
- Kristallographische Strukturen
- Koordinationschemie
- Nanostrukturen
- Materialwissenschaft
Bildung & Lehre
- Geometrie-Unterricht
- Platonische Körper Studien
- Symmetrie-Lehre
- 3D-Geometrie
Kunst & Design
- Geometrische Skulpturen
- Moderne Kunstwerke
- Spielwürfel (W8)
- Dekorative Objekte
Formeln zur Berechnung eines Oktaeders
Volumen (V)
Volumen mit der Quadratwurzel von 2
Oberfläche (S)
8 gleichseitige Dreiecke
Diagonale (d)
Raumdiagonale mit √2
Umkugelradius (R)
Radius der Umkugel
Inkugelradius (r)
Radius der Inkugel
Höhe (h)
Höhe zwischen gegenüberliegenden Ecken
Die √2-Proportionen des Oktaeders
√2 ≈ 1.414
Perfekte Komplementarität
8 gleichseitige Dreiecke
Alle Oktaeder-Proportionen basieren auf der Quadratwurzel von 2
Berechnungsbeispiel für ein Oktaeder
Gegeben
Gesucht: Alle Eigenschaften des Oktaeders
1. Volumen-Berechnung
Für a = 10:
\[V = \frac{10^3 \sqrt{2}}{3}\] \[V ≈ \frac{1000 \cdot 1.414}{3}\] \[V ≈ 471.4\]Das Volumen beträgt etwa 471 Volumeneinheiten
2. Oberflächen-Berechnung
Für a = 10:
\[S = 2 \cdot 10^2 \sqrt{3}\] \[S ≈ 200 \cdot 1.732\] \[S ≈ 346.4\]Die Oberfläche beträgt etwa 346 Flächeneinheiten
3. Diagonale-Berechnung
Für a = 10:
\[d = 10 \sqrt{2}\] \[d ≈ 10 \cdot 1.414\] \[d ≈ 14.14\]Die Diagonale beträgt etwa 14.14 Längeneinheiten
4. Das perfekte Oktaeder
Das Oktaeder mit perfekter √2-Symmetrie
Das Oktaeder: Der Doppel-Pyramiden-Körper
Das Oktaeder ist ein eleganter platonischer Körper, der die Schönheit der doppelten Pyramiden-Struktur verkörpert. Mit seinen 8 gleichseitigen Dreiecken, 6 Ecken und 12 Kanten zeigt es eine einzigartige Verbindung zur Quadratwurzel von 2 (√2 ≈ 1.414). Als Dualkörper zum Würfel bildet es eine perfekte geometrische Komplementarität und demonstriert die elegante Einfachheit mathematischer Beziehungen. Seine Struktur kann als zwei vierseitige Pyramiden verstanden werden, die an ihren Grundflächen zusammengefügt sind.
Die Eleganz der doppelten Pyramiden-Struktur
Das Oktaeder zeigt die perfekte Balance zwischen Einfachheit und Symmetrie:
- Deltaeder: Alle 8 Flächen sind kongruente gleichseitige Dreiecke
- √2-Proportionen: Alle Hauptabmessungen basieren auf √2
- Würfel-Dual: Perfekte duale Beziehung zum Würfel (Hexaeder)
- Platonische Eleganz: Einer der fünf regulären Polyeder
- Doppel-Pyramide: Zwei vierseitige Pyramiden Basis an Basis
- Oktaedrische Symmetrie: Hohe Punktsymmetrie
- Kristallographische Bedeutung: Häufige Kristallform
Mathematische Klarheit
√2-Perfektion
Die Formeln des Oktaeders sind durchdrungen von der Quadratwurzel von 2, was zu einer einzigartigen Klarheit und Eleganz führt.
Triangulare Symmetrie
Die 8 gleichseitigen Dreiecke erzeugen eine perfekte oktaedrische Symmetrie mit hoher Punktsymmetrie.
Duale Beziehung
Als Dual zum Würfel zeigt das Oktaeder die tiefe Verbindung zwischen verschiedenen platonischen Körpern.
Strukturelle Effizienz
Die doppelte Pyramiden-Struktur macht das Oktaeder zu einer idealen Form für strukturelle Anwendungen.
Zusammenfassung
Das Oktaeder verkörpert die Eleganz der geometrischen Einfachheit und steht als perfektes Beispiel für die Schönheit der √2-Proportionen da. Seine Struktur aus 8 gleichseitigen Dreiecken, die sich zu einer doppelten Pyramiden-Form zusammenfügen, macht es zu einem faszinierenden Studienobjekt für Mathematiker, Kristallographen und Ingenieure. Von der reinen Geometrie über Kristallstrukturen bis hin zu strukturellen Anwendungen zeigt das Oktaeder, wie mathematische Klarheit und praktische Effizienz Hand in Hand gehen. Seine √2-basierten Formeln offenbaren die tiefe Verbindung zwischen einfachen mathematischen Konstanten und komplexen geometrischen Formen. Als Dualkörper zum Würfel demonstriert es die harmonische Balance verschiedener geometrischer Prinzipien und bleibt ein zeitloses Beispiel für die Kraft der geometrischen Symmetrie.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder