Keil berechnen
Rechner und Formeln zur Berechnung eines Keils
Keil Rechner
Der Keil
Ein Keil ist ein Prisma mit trapezförmiger Grundfläche und komplexen geometrischen Beziehungen.
Keil Eigenschaften
Der Keilkörper: Prisma mit trapezförmiger Grundfläche
Keil Struktur
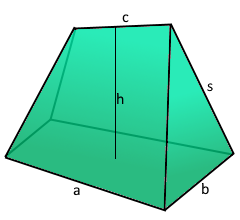
Der vielseitige Keilkörper mit trapezförmiger Grundfläche.
Komplexe Geometrie mit verschiedenen Seitenlängen.
|
|
Was ist ein Keil?
Ein Keil ist ein komplexer geometrischer Körper:
- Definition: Prisma mit trapezförmiger Grundfläche
- Grundfläche: Trapez mit parallelen Seiten a und c
- Seitenflächen: Vier rechteckige und zwei trapezförmige Flächen
- Ecken: 8 Eckpunkte
- Kanten: 12 Kanten verschiedener Längen
- Symmetrie: Spiegelsymmetrie bezüglich einer Mittelebene
Geometrische Eigenschaften des Keils
Der Keil zeigt komplexe geometrische Eigenschaften:
Grundparameter
- Parallele Seiten: Obere Seite a und untere Seite c
- Breite: Konstante Breite b über die gesamte Höhe
- Höhe: Senkrechte Ausdehnung h des Prismas
- Schräge Kante: Verbindung zwischen unterschiedlichen Seitenlängen
Besondere Eigenschaften
- Trapezform: Grundfläche ist ein Trapez
- Prismaform: Gleichmäßige Höhe über gesamte Grundfläche
- Komplexe Oberfläche: Verschiedene Flächentypen
- Praktische Anwendung: Häufig in Technik und Architektur
Mathematische Beziehungen
Der Keil folgt komplexen mathematischen Gesetzmäßigkeiten:
Volumenformel
Komplexe Volumenformel für Trapez-Prisma. Berücksichtigt unterschiedliche Seitenlängen.
Schräge Kante
3D-Pythagoras für die schräge Verbindungskante. Komplexe räumliche Beziehung.
Anwendungen des Keils
Keile finden in vielen praktischen Bereichen Anwendung:
Technik & Industrie
- Maschinenbau und mechanische Keile
- Spannvorrichtungen und Klemmelemente
- Gießerei- und Formenbau
- Werkzeugherstellung
Architektur & Bau
- Dachkonstruktionen und Sparren
- Treppen und Stufen
- Fundamente und Stützelemente
- Brückenbau und Tragwerke
Bildung & Wissenschaft
- Geometrieunterricht und Volumenberechnungen
- Ingenieursausbildung
- 3D-Modellierung und CAD
- Mathematische Demonstrationen
Handwerk & Alltag
- Möbelbau und Tischlerei
- Verpackungsdesign
- Landschaftsgestaltung
- Künstlerische Objekte
Formeln zur Berechnung eines Keils
Volumen V
Volumen des Keilkörpers mit trapezförmiger Grundfläche
Oberfläche S
Komplexe Oberflächenformel mit allen Teilflächen
Schräge Kante s
3D-Pythagoras für die schräge Verbindungskante
Grundfläche AG
Fläche des Trapezes
Mittlere Seite m
Mittellinie des Trapezes
Seitenflächen-Bereiche
A₁ = a · h
A₂ = c · h
A₃ = 2 · s · b
Die verschiedenen Seitenflächen des Keilkörpers
Berechnungsbeispiel für einen Keil
Gegeben
Gesucht: Volumen, Oberfläche und schräge Kante des Keils
1. Grundfläche berechnen
Die Grundfläche beträgt 21 Quadrateinheiten
2. Volumen berechnen
Das Volumen beträgt 55 Kubikeinheiten
3. Schräge Kante berechnen
Die schräge Kante beträgt etwa 5.32 Einheiten
4. Oberfläche berechnen
Die Oberfläche beträgt etwa 144 Quadrateinheiten
5. Keil-Eigenschaften
Der vielseitige Keilkörper mit komplexer Trapez-Geometrie
Der Keil: Der vielseitige Körper der praktischen Geometrie
Der Keil ist einer der vielseitigsten und praktisch wichtigsten geometrischen Körper. Mit seiner trapezförmigen Grundfläche und prismatischen Struktur verkörpert er eine perfekte Verbindung zwischen mathematischer Komplexität und praktischer Anwendbarkeit. Als Prisma mit trapezförmiger Grundfläche repräsentiert er fortgeschrittene Prinzipien der räumlichen Geometrie, wo seine charakteristischen Eigenschaften durch komplexe aber lösbare mathematische Beziehungen beschrieben werden.
Die Geometrie der trapezförmigen Grundfläche
Der Keil fasziniert durch seine asymmetrischen geometrischen Eigenschaften:
- Trapezförmige Grundfläche: Trapez mit parallelen Seiten a und c sowie konstanter Breite b
- Asymmetrische Struktur: Unterschiedliche Seitenlängen schaffen komplexe räumliche Beziehungen
- Prismatische Form: Gleichmäßige Höhe h über der gesamten trapezförmigen Grundfläche
- Komplexe Seitenflächen: Zwei rechteckige und vier trapezförmige bzw. parallelogrammartige Flächen
- Schräge Kanten: 3D-Verbindungslinien zwischen verschiedenen Höhenebenen
- Praktische Formgebung: Ideale Form für technische und architektonische Anwendungen
- Symmetrieeigenschaften: Spiegelsymmetrie bezüglich der Mittelebene bei gleichzeitiger Asymmetrie der Seitenlängen
Prismen und komplexe räumliche Geometrie
Trapez-Prisma-Prinzipien
Als Prisma mit trapezförmiger Grundfläche folgt der Keil erweiterten Prisma-Gesetzmäßigkeiten: variable Querschnittsfläche, parallele aber unterschiedliche Grund- und Deckflächen, komplexe Seitenflächen.
Asymmetrische Geometrie
Die unterschiedlichen Seitenlängen a und c machen alle Berechnungen anspruchsvoller und erfordern die Anwendung erweiterter geometrischer Prinzipien und komplexer Volumenformeln.
Räumliche Komplexität
Der Übergang von der zweidimensionalen Trapezfläche zum dreidimensionalen Keilkörper demonstriert fortgeschrittene Prinzipien der räumlichen Geometrie mit asymmetrischen Elementen.
Erweiterte Mathematik
Die Formeln erfordern komplexere Berechnungen als einfache Prismen, verwenden aber noch immer grundlegende arithmetische Operationen und Quadratwurzeln, ergänzt durch Trapez-spezifische Faktoren.
Mathematische Komplexität und praktische Lösbarkeit
Der Keil zeichnet sich durch ausgewogene mathematische Komplexität aus:
Erweiterte Formeln
Volumen = b·h·(a/3 + c/6) und komplexe Oberflächenformeln erfordern fortgeschrittene mathematische Kenntnisse, bleiben aber für praktische Anwendungen berechenbar.
3D-Pythagoras-Anwendung
Die Berechnung der schrägen Kante erweitert den Satz des Pythagoras in den dreidimensionalen Raum und zeigt komplexe räumliche Beziehungen auf.
Praktische Berechenbarkeit
Trotz erhöhter Komplexität lassen sich alle Parameter mit erweiterten aber standardisierten Methoden berechnen, was den Keil für technische Anwendungen geeignet macht.
Didaktischer Wert
Als Fortführung einfacher Prismen bietet der Keil einen idealen Übergang zu komplexeren geometrischen Körpern und asymmetrischen Strukturen.
Praktische und technische Bedeutung
Der Keil findet breite praktische Anwendungen:
- Maschinenbau: Komplexe Keile als Spannelemente, Führungen und asymmetrische Verbindungselemente
- Bauwesen: Spezielle Dachkonstruktionen, asymmetrische Fundamente und architektonische Gestaltungselemente
- Gießerei: Formen und Kerne für komplexe Gussstücke mit variablen Wandstärken
- Verpackung: Optimierte Raumnutzung und stabile Konstruktionen mit angepassten Formen
- Design: Ästhetische Gestaltungselemente in Architektur und Produktdesign mit asymmetrischen Akzenten
- Bildung: Fortgeschrittenes Verständnis für räumliche Geometrie und komplexe Volumenberechnungen
- Simulation: Realistische Testobjekte für 3D-Modellierung und Finite-Elemente-Methoden mit asymmetrischen Eigenschaften
Herstellung und praktische Realisierung
Fertigungsherausforderungen
Die asymmetrischen geometrischen Formen stellen höhere Anforderungen an die Fertigung. Präzise Winkel und unterschiedliche Seitenlängen erfordern sorgfältige Planung und Ausführung.
Materialoptimierung
Die komplexeren geometrischen Verhältnisse ermöglichen optimierte Materialausnutzung für spezifische Anwendungen, erfordern aber detailliertere Berechnungen.
Erweiterte Qualitätskontrolle
Die unterschiedlichen Maße und asymmetrischen Verhältnisse erfordern spezialisierte Messmethoden und präzise Qualitätskontrolle mit erweiterten Messwerkzeugen.
Anwendungsvielfalt
Durch Variation der Parameter a, b, c und h lässt sich eine große Vielfalt an Keilformen für unterschiedlichste Anwendungen und Funktionen realisieren.
Pädagogische und wissenschaftliche Aspekte
Erweiterte Bildung
Der Keil eignet sich ideal für fortgeschrittenen Geometrieunterricht, da er komplexere Konzepte wie asymmetrische Flächen, erweiterte Volumenberechnungen und räumliche Beziehungen vermittelt.
Komplexe Anschaulichkeit
Die asymmetrischen aber noch überschaubaren Strukturen fordern das räumliche Vorstellungsvermögen heraus und können mit erweiterten Mitteln als Modelle hergestellt werden.
Technische Relevanz
In der angewandten Mathematik und im Ingenieurwesen dienen Keilformen als realistische Grundelemente für komplexere Berechnungsverfahren und praktische Anwendungen.
Transferwert
Die am Keil erlernten erweiterten Prinzipien lassen sich direkt auf noch komplexere asymmetrische geometrische Körper und anspruchsvolle praktische Problemstellungen übertragen.
Zusammenfassung
Der Keil steht als einer der vielseitigsten und praktisch wichtigsten geometrischen Körper da. Seine trapezförmige Grundfläche und asymmetrische prismatische Form, verbunden mit erweiterten aber lösbaren mathematischen Beziehungen, machen ihn zu einem idealen Bindeglied zwischen grundlegender und fortgeschrittener Geometrie. Von seiner Rolle in der technischen Ausbildung bis zu seinen vielfältigen praktischen Anwendungen zeigt er, wie mathematische Komplexität und praktische Vielseitigkeit eine produktive Einheit bilden können. Als Baustein der erweiterten räumlichen Geometrie bleibt er ein unverzichtbares Element für Ingenieure, Architekten, Techniker und alle, die die Schönheit asymmetrischer aber harmonischer geometrischer Formen zu schätzen wissen.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder