Quader Rechner
Rechner und Formeln zur Berechnung des Volumens, der Oberfläche und Diagonale eines Quaders
Quader Rechner
Der Quader
Ein Quader ist ein geometrischer Körper mit sechs rechteckigen Flächen.
Quader Eigenschaften
Der Grundkörper: Sechs rechteckige Flächen in rechtwinkliger Anordnung
Quader Struktur
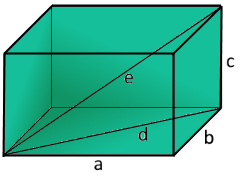
Der vielseitige Grundkörper mit sechs rechteckigen Flächen.
Spezialfall: Würfel bei a = b = c.
|
|
Was ist ein Quader?
Ein Quader ist der fundamentalste geometrische Körper:
- Definition: Körper mit sechs rechteckigen Flächen
- Flächen: Jeweils zwei Flächen sind parallel und kongruent
- Kanten: Alle Kanten treffen sich rechtwinklig
- Ecken: 8 Ecken mit je drei rechtwinkligen Kanten
- Spezialfall: Würfel bei gleichen Kantenlängen
- Koordinaten: Perfekte Ausrichtung zu Koordinatenachsen
Geometrische Eigenschaften des Quaders
Der Quader zeigt fundamentale geometrische Eigenschaften:
Grundstruktur
- Drei Kantenlängen: a, b, c bestimmen den Quader vollständig
- Rechte Winkel: Alle Innenwinkel sind 90°
- Parallelität: Gegenüberliegende Flächen sind parallel
- Kongruenz: Gegenüberliegende Flächen sind kongruent
Besondere Eigenschaften
- Orthogonalität: Alle Kanten stehen senkrecht aufeinander
- Symmetrie: Punktsymmetrie bezüglich des Mittelpunkts
- Euler-Charakteristik: V - E + F = 8 - 12 + 6 = 2
- Koordinatengeometrie: Ideal für kartesische Koordinaten
Mathematische Beziehungen
Der Quader folgt einfachen aber fundamentalen mathematischen Gesetzen:
Volumen V
Das Produkt aller drei Kantenlängen. Einfachste Volumenformel in der Geometrie.
Oberfläche S
Summe aller sechs Rechteckflächen. Jede Fläche kommt zweimal vor.
Anwendungen des Quaders
Quader finden in unzähligen praktischen Bereichen Anwendung:
Bauwesen & Architektur
- Grundrisse und Raumvolumen
- Materialbedarfs-Kalkulationen
- Betonfundamente und Bauteile
- Lagerhallen und Containerbau
Industrie & Logistik
- Verpackungsdesign und Kartons
- Lagerkapazität und Palettenoptimierung
- Transport- und Frachtberechnung
- Behälter und Tanks
Technik & Design
- 3D-Modellierung und CAD-Design
- Elektronikgehäuse und Computerkomponenten
- Möbeldesign und Innenarchitektur
- Maschinenbau und Prototyping
Bildung & Wissenschaft
- Geometrie-Unterricht und Grundlagen
- Mathematische Modellierung
- Physikalische Experimente
- Raumgeometrie und Koordinatensysteme
Formeln für den Quader
Volumen V
Das Produkt aller drei Kantenlängen
Oberfläche S
Summe aller sechs Rechteckflächen
Flächendiagonale d
Diagonale einer rechteckigen Seitenfläche
Raumdiagonale e
Diagonale durch den gesamten Quader
Weitere Eigenschaften
\[U = 2(a + b)\]
\[A_{Grund} = a \cdot b\]
\[A_{Mantel} = 2c(a + b)\]
Zusätzliche geometrische Eigenschaften des Quaders
Spezialfälle
a = b = c
a = b ≠ c
a ≠ b ≠ c
Verschiedene Ausprägungen des Quaders basierend auf den Kantenverhältnissen
Berechnungsbeispiel für einen Quader
Gegeben
Gesucht: Alle Eigenschaften des Quaders
1. Volumen berechnen
Das Volumen beträgt 60 Kubikzentimeter
2. Oberfläche berechnen
Die Oberfläche beträgt 94 Quadratzentime
3. Flächendiagonale
Die Flächendiagonale beträgt etwa 6,40 cm
4. Raumdiagonale
Die Raumdiagonale beträgt etwa 7,07 cm
5. Zusammenfassung aller Ergebnisse
Der fundamentale geometrische Körper mit seinen charakteristischen Eigenschaften
Der Quader: Der fundamentale geometrische Körper
Der Quader ist zweifellos der fundamentalste und praktisch wichtigste geometrische Körper in unserer Welt. Mit seinen sechs rechteckigen Flächen, acht Ecken und zwölf Kanten verkörpert er die Essenz orthogonaler Geometrie und bildet das Grundgerüst für unzählige Anwendungen von der Architektur bis zur Logistik. Seine mathematische Einfachheit kombiniert mit seiner praktischen Vielseitigkeit macht ihn zu einem unverzichtbaren Werkzeug in Wissenschaft, Technik und täglichem Leben.
Die Geometrie des Quaders
Der Quader fasziniert durch seine strukturelle Klarheit:
- Sechs Rechteckflächen: Jeweils zwei parallele und kongruente Flächen
- Rechte Winkel: Alle 24 Innenwinkel sind exakt 90°
- Drei Kantenlängen: a, b, c bestimmen den Quader vollständig
- Orthogonale Kanten: Alle Kanten stehen senkrecht aufeinander
- Punktsymmetrie: Symmetrie bezüglich des Mittelpunkts
- Koordinatenausrichtung: Perfekte Passung zu kartesischen Koordinaten
- Euler-Charakteristik: V - E + F = 8 - 12 + 6 = 2
Mathematische Eleganz
Einfache Formeln
Die Volumenformel V = a·b·c ist die einfachste Volumenberechnung überhaupt. Diese mathematische Eleganz macht den Quader zum idealen Ausgangspunkt für geometrische Studien.
Pythagoras-Anwendung
Die Diagonalberechnungen zeigen perfekte Anwendungen des Satzes von Pythagoras: erst in der Fläche (d = √(a²+b²)), dann im Raum (e = √(a²+b²+c²)).
Proportionalität
Alle Eigenschaften skalieren vorhersagbar: Verdopplung einer Kante verdoppelt bestimmte Flächen und das Volumen entsprechend, was in der Praxis entscheidend ist.
Optimierungspotential
Bei gegebenem Volumen minimiert der Würfel (a=b=c) die Oberfläche - ein fundamentales Optimierungsprinzip in Natur und Technik.
Praktische Bedeutung in Technik und Alltag
Der Quader ist omnipräsent in unserem täglichen Leben:
Bauwesen
Von Ziegeln über Betonblöcke bis zu Raumvolumen - der Quader ist das Grundelement der Architektur. Seine rechtwinklige Struktur ermöglicht effiziente Raumnutzung und einfache Konstruktion.
Verpackung
Kartons, Container und Verpackungen nutzen die Quaderform für optimale Stapelbarkeit und Transporteffizienz. Die rechteckige Form maximiert Raumnutzung bei minimaler Verschwendung.
Technologie
Elektronikgehäuse, Computerkomponenten und Bildschirme nutzen die Quaderform für Standardisierung und effiziente Herstellung. Die orthogonale Struktur vereinfacht Design und Produktion.
Logistik
Paletten, Lagerregale und Transportbehälter basieren auf Quadergeometrie für optimale Raumausnutzung und systematische Lagerung großer Mengen.
Historische Entwicklung und kulturelle Bedeutung
Die Bedeutung des Quaders zieht sich durch die gesamte Menschheitsgeschichte:
- Antike Bauten: Pyramiden und Tempel nutzten Quaderblöcke als Grundbausteine
- Römische Architektur: Systematische Verwendung von Quadersteinen für monumentale Bauten
- Industrialisierung: Standardisierung durch rechteckige Bauteile und Module
- Moderne Architektur: Bauhaus und funktionalistische Bewegungen
- Digitales Zeitalter: Pixel, Voxel und digitale Raster basieren auf Quaderstrukturen
- Nachhaltigkeit: Optimierte Materialnutzung durch effiziente Quadergeometrie
- Zukunftsvision: Modulares Bauen und 3D-Druck mit Quader-Elementen
Spezialfälle und Variationen
Der Würfel
Als Spezialfall mit a=b=c ist der Würfel der symmetrischste Quader. Er minimiert bei gegebenem Volumen die Oberfläche und maximiert bei gegebener Oberfläche das Volumen.
Quadratisches Prisma
Bei a=b≠c entsteht ein quadratisches Prisma, das in Architektur und Design häufig für Säulen, Türme und vertikale Strukturen verwendet wird.
Flacher Quader
Bei sehr kleinem c entsteht eine quaderförmige Platte, wie sie in der Elektronik, bei Bildschirmen oder als Bodenplatten verwendet wird.
Länglicher Quader
Bei stark unterschiedlichen Kantenlängen entstehen Balken oder Stäbe, die in der Konstruktionstechnik als Träger und Verstrebungen dienen.
Mathematische Verallgemeinerungen
Höhere Dimensionen
Der Quader verallgemeinert sich zum Hyperquader in n Dimensionen, was in der Mathematik und Computergrafik für Datenstrukturen und Algorithmen fundamental ist.
Koordinatengeometrie
Als achsenparalleler Körper ist der Quader ideal für kartesische Koordinatensysteme und bildet die Basis für Rasterstrukturen in Computer-Grafik und Numerik.
Diskrete Geometrie
In der digitalen Welt werden Pixel (2D) und Voxel (3D) als kleinste Quader-Einheiten verwendet, die komplexe Strukturen durch Kombination einfacher Rechtecke/Quader approximieren.
Optimierung
Quaderförmige Begrenzungen sind in der Optimierungstheorie und im Operations Research fundamental für die Formulierung von Beschränkungen und Zielfunktionen.
Pädagogische und kulturelle Bedeutung
Bildungswert
Der Quader ist der ideale Einstieg in die Raumgeometrie. Seine einfachen, aber vollständigen Eigenschaften vermitteln alle wichtigen Konzepte der 3D-Geometrie ohne überflüssige Komplexität.
Abstraktionsfähigkeit
Das Verständnis des Quaders entwickelt räumliches Vorstellungsvermögen und bildet die Grundlage für das Verstehen komplexerer geometrischer Körper.
Kulturelle Symbolik
In vielen Kulturen symbolisiert die rechteckige Form Ordnung, Stabilität und Beständigkeit. Von der ägyptischen Architektur bis zur modernen Kunst ist der Quader ein Symbol für Struktur.
Universalität
Als universell verständliche Form überwindet der Quader kulturelle Grenzen und ermöglicht internationale Standards in Technik, Architektur und Design.
Zusammenfassung
Der Quader steht als Paradebeispiel für die Eleganz der Einfachheit in der Geometrie. Seine sechs rechteckigen Flächen, geordnet in perfekter orthogonaler Harmonie, machen ihn zum vielseitigsten und praktisch wichtigsten geometrischen Körper. Von der antiken Architektur bis zur modernen Digitaltechnik, von der Grundschulmathematik bis zur komplexen Optimierungstheorie - der Quader zeigt, wie mathematische Klarheit und praktische Anwendbarkeit eine untrennbare Einheit bilden können. Als Fundament der räumlichen Geometrie und Basis unzähliger technischer Innovationen wird der Quader auch in Zukunft seine zentrale Rolle in Wissenschaft, Technik und täglichem Leben behalten. Seine zeitlose Einfachheit ist zugleich seine größte Stärke.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder