Unregelmäßiges Tetraeder Rechner
Rechner und Formeln zur Berechnung eines unregelmäßigen Tetraeders
Tetraeder Rechner
Das Unregelmäßige Tetraeder
Ein Tetraeder ist eine dreidimensionale Pyramide mit 4 Dreiecken, 6 Kanten und 4 Ecken.
Tetraeder Eigenschaften
Die 3D-Pyramide: Einfachster dreidimensionaler Körper
Tetraeder Struktur
Die einfachste 3D-Form mit 4 Dreiecken.
Grundbaustein der 3D-Geometrie.
|
|
Was ist ein unregelmäßiges Tetraeder?
Ein unregelmäßiges Tetraeder ist die allgemeinste Form eines Tetraeders:
- Definition: Polyeder mit 4 dreieckigen Flächen unterschiedlicher Größe
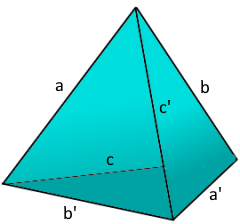
- Kanten: 6 Kanten mit beliebigen Längen (a, b, c, a', b', c')
- Grundform: Einfachster dreidimensionaler Körper
- Ecken: 4 Ecken mit verschiedenen Winkeln
- Flächen: 4 Dreiecke unterschiedlicher Flächeninhalte
- Besonderheit: Vollständig durch 6 Kantenlängen bestimmt
Geometrische Eigenschaften des Tetraeders
Das unregelmäßige Tetraeder zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Kantenlängen: Sechs verschiedene Kantenlängen möglich
- Flächen: 4 Dreiecke mit unterschiedlichen Flächeninhalten
- Euler-Charakteristik: V - E + F = 4 - 6 + 4 = 2
- Topologie: Einfachste konvexe 3D-Form
Besondere Eigenschaften
- Simplex: 3-dimensionaler Simplex (3-Simplex)
- Grundbaustein: Basis für Tetraedernetze in der FEM
- Flexibilität: Große Variabilität bei 6 freien Parametern
- Robustheit: Stabilste 3D-Struktur in der Statik
Mathematische Beziehungen
Das unregelmäßige Tetraeder folgt komplexen mathematischen Formeln:
Volumenformel
Mit Cayley-Menger-Determinante Δ. Komplexe Formel mit 6 Kantenlängen.
Oberflächenformel
Summe der 4 Dreiecksflächen. Jede nach Heron'scher Formel berechnet.
Anwendungen des Tetraeders
Tetraeder finden vielfältige Anwendungen:
Wissenschaft & Technik
- Finite-Elemente-Methode (FEM) in der Strukturanalyse
- Kristallographie und Molekularstrukturen
- 3D-Computergrafik und Rendering
- Baustatik und Fachwerke
Mathematik & Informatik
- Delaunay-Triangulation in der Geometrie
- Volumenberechnungen in CAD-Software
- Optimierungsalgorithmen
- Topologische Studien
Bildung & Lehre
- Geometrie-Unterricht und 3D-Visualisierung
- Grundlagen der Raumgeometrie
- Vektorrechnung und analytische Geometrie
- Mathematische Modellierung
Architektur & Design
- Architektonische Strukturen und Dachkonstruktionen
- Skulpturale und künstlerische Installationen
- Produktdesign und Industriedesign
- Verpackungsdesign und Optimierung
Formeln für das unregelmäßige Tetraeder
Volumen V (Cayley-Menger-Determinante)
Die allgemeine Volumenformel für 6 beliebige Kantenlängen
Oberfläche S (Heron'sche Formel für Dreiecke)
Summe der vier Dreiecksflächen nach Heron's Formel
Kantenlängen-Schema
△₁: a, b, c
△₂: a, b', c'
△₃: a', b, c'
△₄: a', b', c
Zuordnung der 6 Kanten zu den 4 Dreiecken
Euler-Charakteristik
4 - 6 + 4 = 2
✓ Topologisch korrekt
Grundlegende topologische Eigenschaft
Berechnungsbeispiel für ein unregelmäßiges Tetraeder
Gegeben
Gesucht: Volumen und Oberfläche des Tetraeders
1. Volumenberechnung
Berechnung der Hilfswerte fa, fb, fc
2. Weitere Berechnung
Berechnung der Deltawerte
3. Endvolumen
Das Volumen beträgt etwa 0.90 Kubikeinheiten
4. Oberflächenberechnung
Die Oberfläche beträgt etwa 87.76 Flächeneinheiten
5. Tetraeder-Eigenschaften
Die grundlegende 3D-Form mit komplexer mathematischer Struktur
Das Tetraeder: Der fundamentale Baustein der 3D-Geometrie
Das Tetraeder ist der einfachste dreidimensionale Körper und bildet die Grundlage der gesamten 3D-Geometrie. Mit nur 4 Ecken, 6 Kanten und 4 dreieckigen Flächen verkörpert es die minimale Struktur eines Volumenkörpers. Als 3-dimensionaler Simplex spielt es eine fundamentale Rolle in der Mathematik, von der algebraischen Topologie bis zur numerischen Analysis. Jedes Tetraeder ist vollständig durch seine 6 Kantenlängen bestimmt und kann durch die komplexe Cayley-Menger-Determinante berechnet werden.
Die Geometrie des Simplex
Das Tetraeder fasziniert durch seine fundamentalen geometrischen Eigenschaften:
- Minimale 3D-Struktur: Kleinstmöglicher Volumenkörper mit 4 Punkten im Raum
- Simplex-Eigenschaft: 3-dimensionaler Simplex, Verallgemeinerung des Dreiecks
- Sechs Parameter: Vollständig bestimmt durch 6 Kantenlängen (a, b, c, a', b', c')
- Vier Flächen: Jede Fläche ist ein Dreieck, bestimmt durch 3 Kanten
- Euler-Formel: V - E + F = 4 - 6 + 4 = 2 (topologische Invariante)
- Konvexität: Jeder Punkt im Inneren liegt auf der konvexen Hülle der 4 Ecken
- Rigidität: Bei gegebenen Kantenlängen eindeutig bestimmt (bis auf Spiegelung)
Mathematische Grundlagen
Cayley-Menger-Determinante
Die Volumenberechnung basiert auf der Cayley-Menger-Determinante, die aus den paarweisen Abständen der 4 Eckpunkte gebildet wird. Diese elegante mathematische Struktur verbindet Metrik und Volumen.
Heron'sche Formel
Die Oberfläche wird durch Summation der vier Dreiecksflächen berechnet, jede nach der klassischen Heron'schen Formel bestimmt. Dies zeigt die Verbindung zwischen 2D- und 3D-Geometrie.
Topologische Struktur
Als einfachstes Polyeder zeigt das Tetraeder die grundlegenden topologischen Eigenschaften: Die Euler-Charakteristik χ = 2 ist invariant unter kontinuierlichen Verformungen.
Geometrische Constraints
Nicht jede Kombination von 6 Kantenlängen führt zu einem realisierbaren Tetraeder. Die Dreiecksungleichungen und weitere Constraints müssen erfüllt sein.
Das Tetraeder in der Numerik
Das Tetraeder spielt eine zentrale Rolle in der numerischen Mathematik:
Finite-Elemente-Methode
Tetraeder sind die Standardelemente für 3D-FEM-Berechnungen. Ihre einfache Geometrie ermöglicht effiziente Implementierungen und robuste numerische Algorithmen in der Strukturmechanik.
Delaunay-Triangulation
In der 3D-Delaunay-Triangulation werden Punktwolken optimal in Tetraeder zerlegt. Diese Methode ist fundamental für Mesh-Generierung und geometrische Modellierung.
Volumenintegration
Komplexe 3D-Bereiche werden in Tetraeder zerlegt, um Volumenintegrale numerisch zu berechnen. Die einfache Geometrie ermöglicht effiziente Quadraturformeln.
Computergrafik
In der 3D-Computergrafik dienen Tetraeder zur Volumenvisualisierung und als primitive Grundbausteine für komplexere Geometrien.
Wissenschaftliche und technische Bedeutung
Das Tetraeder findet vielfältige wissenschaftliche Anwendungen:
- Kristallographie: Tetraedrische Koordination in Kristallstrukturen (Diamant, Silicate)
- Molekulargeometrie: Sp³-Hybridisierung und tetraedrische Molekülstrukturen
- Baustatik: Tetraeder-Fachwerke als stabilste 3D-Konstruktionen
- Robotik: Tetraeder-Roboter und rekonfigurierbare Strukturen
- Materialwissenschaft: Tetraeder-Packungen und Schaumstrukturen
- Geodäsie: Triangulationsnetze und Satellitentriangulation
- Biologie: Tetraedrische Strukturen in Viren und Proteinen
Konstruktion und praktische Herausforderungen
Realisierbarkeit
Nicht jede Kombination von 6 Kantenlängen führt zu einem realisierbaren Tetraeder. Die Gram-Matrix muss positiv semidefinit sein, was komplexe algebraische Bedingungen impliziert.
Numerische Stabilität
Die Berechnung der Cayley-Menger-Determinante ist numerisch anspruchsvoll, besonders bei fast-planaren Konfigurationen. Spezielle Algorithmen sind für robuste Implementierungen erforderlich.
Optimierungsprobleme
Tetraeder-Optimierung (maximales Volumen bei gegebener Oberfläche) führt zu komplexen nichtlinearen Optimierungsproblemen mit praktischen Anwendungen in Design und Engineering.
Qualitätsmessung
In der FEM ist die Tetraeder-Qualität entscheidend. Aspekt-Verhältnis, Volumen-zu-Oberflächenverhältnis und andere Qualitätsmaße bestimmen die numerische Stabilität.
Philosophische und historische Perspektiven
Historische Bedeutung
Das Tetraeder war bereits den antiken Griechen bekannt und gehört zu den platonischen Körpern (regelmäßiges Tetraeder). Es symbolisierte das Element Feuer und verkörperte geometrische Perfektion.
Dimensional Scaling
Als 3D-Simplex verallgemeinert das Tetraeder das Konzept des Dreiecks in höhere Dimensionen. Der n-Simplex ist ein fundamentales Konzept in der algebraischen Topologie.
Symmetrie und Schönheit
Das regelmäßige Tetraeder verkörpert mathematische Schönheit durch seine hohe Symmetrie. Diese ästhetische Dimension verbindet Mathematik, Kunst und Architektur.
Fundamentale Struktur
Als einfachster Volumenkörper steht das Tetraeder für die Essenz der 3D-Geometrie. Es zeigt, wie aus minimalen Komponenten komplexe Strukturen entstehen können.
Zusammenfassung
Das Tetraeder steht als fundamentaler Baustein der 3D-Geometrie da. Seine scheinbare Einfachheit - nur 4 Ecken, 6 Kanten und 4 Flächen - verbirgt eine reiche mathematische Struktur, die von der Cayley-Menger-Determinante bis zur topologischen Invarianz reicht. Von der antiken Geometrie bis zur modernen numerischen Analysis, von der Kristallographie bis zur Computergrafik zeigt das Tetraeder seine universelle Bedeutung. Als 3D-Simplex verkörpert es die Essenz der dreidimensionalen Geometrie und bleibt ein unverzichtbares Werkzeug für Wissenschaftler, Ingenieure und Mathematiker. Seine Rolle in der Finite-Elemente- Methode und der geometrischen Modellierung macht es zu einem der wichtigsten geometrischen Objekte in der angewandten Mathematik.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder