Dodekaederstern berechnen

Rechner und Formeln zur Berechnung eines Dodekaedersterns


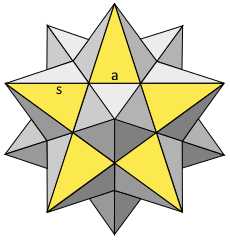
Diese Funktion berechnet verschiedene Parameter eines Dodekaederstern.

Wählen Sie die Eigenschaft aus die Ihnen bekannt ist und geben Sie deren Wert ein. Anschließend klicken Sie auf 'Berechnen'.


Dodekaederstern berechnen

 Eingabe
Dezimalstellen
  Resultate
Seitenlänge a
Kantenlänge s
Volumen V
Oberfläche S
Umkreisradius r
Höhe h

Dodekaederstern

Formeln zur Berechnung eines Dodekaedersterns


Kantenlänge (\(\small{s}\))

\(\displaystyle s = \frac{a}{2} \cdot (1 + \sqrt{5})\) \(\displaystyle \;\;\; ≈ a \cdot 1,618\)

Volumen (\(\small{V}\))

\(\displaystyle V=\frac{5}{4} \cdot a^3 \cdot (7 + 3 \cdot \sqrt{5})\) \(\displaystyle \;\;\; ≈ a^3 \cdot 17.135\)

Oberfläche (\(\small{S}\))

\(\displaystyle S= 15\cdot a^2 \cdot \sqrt{5 + 2 \cdot \sqrt{5}}\) \(\displaystyle \;\;\; ≈ a^2 \cdot 46.165\)

Umkreisradius (\(\small{r}\))

\(\displaystyle r=\frac{a}{4} \cdot \sqrt{50 + 22 \cdot \sqrt{5}}\) \(\displaystyle \;\;\; ≈ a \cdot 2.49\)

Höhe (\(\small{h}\))

\(\displaystyle h = \frac{a}{5} \cdot \sqrt{25 + 10\cdot \sqrt{5}}\) \(\displaystyle \;\;\; ≈ a \cdot 1.3764 \)

Quader • Quadratische Säule • Antiprisma • Sechseckprisma • Dreiecksprisma • Regelmäßiges Prisma • Schiefes Prisma • Rampe • Antiwürfel • Keil • Gerader Keil • Rhomboeder • Parallelepiped • Tetraeder, allgemeines • Pentagonales Trapezoeder • Tetragonales Trapezoeder • Prismatoid • Sterntetraeder • Dodekaederstern • Ikosaederstern • Großes Dodekaeder
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder


Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?