Tetragonales Trapezoeder Rechner
Rechner und Formeln zur Berechnung eines regelmäßigen tetragonalen Trapezoeder
Tetragonales Trapezoeder Rechner
Das Tetragonale Trapezoeder
Ein Tetragonales Trapezoeder ist eine verdrehte Doppelpyramide mit 8 drachenförmigen Flächen.
Trapezoeder Eigenschaften
Die verdrehte Doppelpyramide: Antiprisma um 45° verdreht
Trapezoeder Struktur
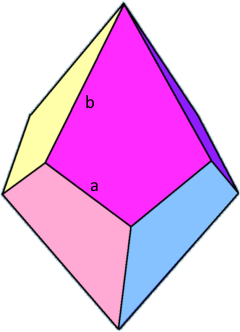
Die elegante verdrehte Doppelpyramide.
8 identische Drachenflächen.
|
|
Was ist ein tetragonales Trapezoeder?
Ein tetragonales Trapezoeder ist eine besondere Form einer verdrehten Doppelpyramide:
- Definition: Polyeder aus 8 identischen drachenförmigen Flächen
- Struktur: Verdrehte Doppelpyramide um 45° (180°/4)
- Symmetrie: 4-fache Rotationssymmetrie um die Hauptachse
- Ecken: 10 Ecken (2 polare + 8 äquatoriale)
- Kanten: 16 Kanten in zwei verschiedenen Längen
- Alternative Namen: Deltoeder, Trapezoeder
Geometrische Eigenschaften des Trapezoeders
Das tetragonale Trapezoeder zeigt faszinierende geometrische Eigenschaften:
Grundparameter
- Kantenlängen: Zwei verschiedene Kantenlängen a und b
- Antiprisma z: Charakteristische Länge der Grundfläche
- Euler-Charakteristik: V - E + F = 10 - 16 + 8 = 2
- Dualität: Dual zum quadratischen Antiprisma
Besondere Eigenschaften
- Verdrehung: Um 45° verdrehte Doppelpyramide
- Drachenflächen: 8 identische kongruente Drachen
- Symmetriegruppe: D₄ (diedrische Gruppe)
- Kristallform: Kommt in der Kristallographie vor
Mathematische Beziehungen
Das tetragonale Trapezoeder folgt eleganten mathematischen Formeln:
Volumenformel
Basiert auf der charakteristischen Länge z. Koeffizient ≈ 0.957 aus der Symmetrie.
Oberflächenformel
Summe von 8 Drachenflächen. Involviert √2 in komplexer Form.
Anwendungen des Trapezoeders
Tetragonale Trapezoeder finden vielfältige Anwendungen:
Wissenschaft & Technik
- Kristallographie und Mineralogische Strukturen
- Optische Elemente und Prismen
- 3D-Druck und rapid Prototyping
- Strukturelle Analyse und FEM
Design & Architektur
- Architektonische Gestaltungselemente
- Dekorative Objekte und Schmuck
- Industriedesign und Produktgestaltung
- Computergrafik und 3D-Modellierung
Bildung & Mathematik
- Geometrie-Unterricht und Demonstrationen
- Symmetrie-Studien und Gruppentheorie
- Dualitäts-Prinzipien in der Polyedertheorie
- Kombinatorische Geometrie
Spiele & Unterhaltung
- Besondere Würfel und Spielwürfel
- Puzzle und mechanische Rätsel
- Künstlerische Skulpturen
- Mathematische Sammlerobjekte
Formeln für das tetragonale Trapezoeder
Seitenlänge a
Kurze Kante der Drachenflächen
Seitenlänge b
Lange Kante der Drachenflächen
Höhe h
Höhe zwischen den polaren Ecken
Oberfläche S
Summe der 8 Drachenflächen
Volumen V
Rauminhalt der verdrehten Doppelpyramide
Antiprisma-Parameter z
Der Parameter z ist die charakteristische Länge der quadratischen Grundfläche des zugrundeliegenden Antiprismas. Alle anderen Größen werden durch Vielfache von z ausgedrückt, wobei √2 eine zentrale Rolle spielt.
Grundparameter für alle Berechnungen
Berechnungsbeispiel für ein tetragonales Trapezoeder
Gegeben
Gesucht: Alle Eigenschaften des Trapezoeders
1. Seitenlängen berechnen
Kurze Kante a ≈ 6.44, lange Kante b ≈ 10.99
2. Höhe berechnen
Die Höhe beträgt etwa 20.30 Einheiten
3. Oberfläche berechnen
Die Oberfläche beträgt etwa 553 Flächeneinheiten
4. Volumen berechnen
Das Volumen beträgt etwa 957 Kubikeinheiten
5. Trapezoeder-Eigenschaften
Die elegante verdrehte Doppelpyramide mit 4-facher Symmetrie
Das Tetragonale Trapezoeder: Die elegante verdrehte Doppelpyramide
Das tetragonale Trapezoeder ist ein faszinierendes geometrisches Objekt, das die Eleganz mathematischer Symmetrie mit praktischer Anwendbarkeit verbindet. Als verdrehte Doppelpyramide um 45° verkörpert es das Prinzip der Antiprisma-Konstruktion und zeigt, wie aus einfachen geometrischen Operationen komplexe und ästhetisch ansprechende Formen entstehen können. Mit seinen 8 identischen drachenförmigen Flächen steht es exemplarisch für die Schönheit regulärer Polyeder und deren Rolle in Wissenschaft, Kunst und Technik.
Die Geometrie der Verdrehung
Das tetragonale Trapezoeder fasziniert durch seine einzigartige Konstruktionsprinzip:
- Antiprisma-Struktur: Entsteht durch 45°-Verdrehung einer quadratischen Doppelpyramide
- 8 Drachenflächen: Jede Fläche ist ein konvexes Viereck mit zwei Paar gleichen Seiten
- Zwei Kantenlängen: Kurze Kanten (a) und lange Kanten (b) in harmonischem Verhältnis
- 10 Ecken: 2 polare Ecken und 8 äquatoriale Ecken in regelmäßiger Anordnung
- D₄-Symmetrie: 4-fache Rotationssymmetrie mit Spiegelungsebenen
- Charakteristische Länge z: Grundparameter des zugrundeliegenden Antiprismas
- √2-Beziehungen: Alle Formeln enthalten √2 als fundamentale Konstante
Trapezoeder und Dualität
Antiprisma-Dualität
Das tetragonale Trapezoeder ist dual zum quadratischen Antiprisma. Diese Dualität zeigt sich in der systematischen Vertauschung von Ecken und Flächen: 10 Ecken ↔ 10 Flächen, während die Kantenzahl (16) invariant bleibt.
Kristallographische Bedeutung
In der Kristallographie tritt das Trapezoeder als natürliche Wachstumsform bei tetragonalen Kristallsystemen auf, wo es die symmetrischen Eigenschaften des Kristallgitters widerspiegelt.
Mathematische Eleganz
Die Formeln zeigen eine bemerkenswerte mathematische Eleganz: Alle Größen sind Vielfache der charakteristischen Länge z, multipliziert mit irrationalen Koeffizienten, die √2 enthalten.
Konstruktive Geometrie
Das Trapezoeder demonstriert die Kraft konstruktiver Geometrie: Durch einfache Verdrehung einer bekannten Form (Doppelpyramide) entsteht ein völlig neues geometrisches Objekt mit eigenen Eigenschaften.
Die Rolle der Quadratwurzel aus 2
Das tetragonale Trapezoeder ist durchdrungen von der Konstante √2:
Fundamentale Konstante
√2 ≈ 1.414 tritt in allen Formeln auf und resultiert aus der 45°-Verdrehung (45° = π/4, cos(π/4) = sin(π/4) = 1/√2). Diese Konstante verbindet das Trapezoeder mit der quadratischen Geometrie.
Proportionale Harmonien
Die Verhältnisse der Kantenlängen a:b ≈ 0.644:1.099 entstehen aus √2-basierten Konstruktionen und erzeugen die charakteristische ästhetische Proportion der Drachenflächen.
Geometrische Interpretation
√2 repräsentiert die Diagonale eines Einheitsquadrats und manifestiert sich im Trapezoeder als natürliche Folge der quadratischen Grundsymmetrie und der 45°-Verdrehung.
Numerische Stabilität
Die √2-basierten Formeln sind numerisch robust und erlauben präzise Berechnungen ohne Rundungsfehler-Akkumulation, was das Trapezoeder zu einem idealen Testobjekt für geometrische Algorithmen macht.
Wissenschaftliche und kulturelle Bedeutung
Das tetragonale Trapezoeder findet vielfältige Anwendungen:
- Kristallographie: Natürliche Wachstumsform bei Mineralien mit tetragonaler Symmetrie
- Optik: Basis für spezielle Prismen und optische Elemente
- Architektur: Inspirationsquelle für moderne Gebäudeformen und Fassadenelemente
- Spieltheorie: Grundlage für besondere Würfel mit 10 Seiten (d10 Zocchihedron)
- Kunst: Skulpturale Arbeiten und geometrische Kunstinstallationen
- Ingenieurswesen: Strukturelle Elemente mit optimierter Festigkeit
- Mathematik: Studienobjekt für Symmetriegruppen und Polyedertheorie
Herstellung und praktische Aspekte
Konstruktive Realisierung
Die Herstellung eines präzisen Trapezoeders erfordert sorgfältige Beachtung der irrationalen Verhältnisse. Moderne CAD-Software und CNC-Fertigung ermöglichen heute die Realisierung mit hoher Genauigkeit.
Materialoptimierung
Das günstige Verhältnis von Volumen zu Oberfläche macht das Trapezoeder attraktiv für materialeffiziente Konstruktionen, besonders in der Verpackungsindustrie und im Leichtbau.
3D-Druck Anwendungen
Das Trapezoeder ist ein beliebtes Testobjekt für 3D-Drucker, da es komplexe Geometrie mit glatten Flächen und scharfen Kanten kombiniert und so die Qualität des Druckers prüft.
Qualitätskontrolle
Die präzisen mathematischen Beziehungen zwischen allen Parametern machen das Trapezoeder zu einem idealen Referenzobjekt für geometrische Messungen und Kalibrierungen.
Philosophische und ästhetische Dimensionen
Symmetrie und Ordnung
Das Trapezoeder verkörpert die mathematische Schönheit regulärer Symmetrie. Seine 4-fache Rotationssymmetrie und die identischen Drachenflächen schaffen eine Harmonie zwischen Komplexität und Ordnung.
Verdrehung als Prinzip
Die 45°-Verdrehung als konstruktives Prinzip zeigt, wie aus bekannten Formen durch einfache Transformationen völlig neue Objekte mit eigenen ästhetischen Qualitäten entstehen können.
Kulturelle Symbolik
In verschiedenen Kulturen symbolisiert das Trapezoeder Transformation und Wandel. Die verdrehte Struktur wird als Metapher für Veränderung und Entwicklung interpretiert.
Pädagogischer Wert
Als Demonstrationsobjekt für Symmetrie, Dualität und konstruktive Geometrie bietet das Trapezoeder hervorragende Möglichkeiten für den Mathematik- und Geometrieunterricht.
Zusammenfassung
Das tetragonale Trapezoeder steht als elegantes Beispiel für die Schönheit und Anwendbarkeit mathematischer Geometrie. Seine Entstehung durch die einfache 45°-Verdrehung einer Doppelpyramide zeigt, wie grundlegende geometrische Operationen zu komplexen und ästhetisch ansprechenden Formen führen können. Die durchgängige Präsenz der Konstante √2 in allen Formeln offenbart die tiefe Verbindung zur quadratischen Geometrie und verleiht dem Trapezoeder eine besondere mathematische Eleganz. Von der Kristallographie bis zur modernen Architektur, von der Spieltheorie bis zur künstlerischen Gestaltung zeigt das tetragonale Trapezoeder seine universelle Relevanz und bleibt ein faszinierendes Studienobjekt für alle, die sich für die Verbindung zwischen Mathematik, Natur und Kunst interessieren.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder