Dreiecksprisma Rechner
Rechner und Formeln zur Berechnung eines regelmäßigen Dreiecksprismas
Dreiecksprisma Rechner
Das Dreiecksprisma
Ein Dreiecksprisma ist ein prismatischer Körper mit gleichseitigen dreieckigen Grundflächen.
Dreiecksprisma Eigenschaften
Das dreieckige Prisma: Zwei gleichseitige Dreiecke als Grundflächen
Dreiecksprisma Struktur
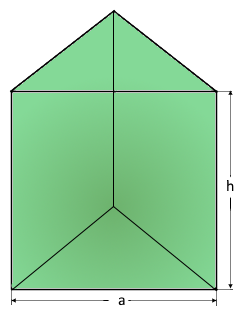
Das regelmäßige Dreiecksprisma mit gleichseitigen Grundflächen.
Basiert auf gleichseitigen Dreiecken.
|
|
Was ist ein Dreiecksprisma?
Ein regelmäßiges Dreiecksprisma ist ein geometrischer Körper:
- Grundflächen: Zwei kongruente gleichseitige Dreiecke
- Seitenflächen: Drei kongruente Rechtecke
- Parallel: Grundflächen liegen parallel zueinander
- Ecken: 6 Ecken insgesamt
- Kanten: 9 Kanten (6+3)
- Flächen: 5 Flächen (2+3)
Geometrische Eigenschaften des Dreiecksprismas
Das regelmäßige Dreiecksprisma zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Grundfläche: Gleichseitiges Dreieck mit Seitenlänge a
- Deckfläche: Identisches gleichseitiges Dreieck
- Euler-Charakteristik: V - E + F = 6 - 9 + 5 = 2
- Prismatyp: Gerades regelmäßiges Prisma
Besondere Eigenschaften
- Regelmäßigkeit: Alle Grundflächenseiten gleich
- Parallelität: Grundflächen parallel zueinander
- Rechteckige Seiten: Drei kongruente Rechtecke
- Symmetrie: Dreifache Rotationssymmetrie
Mathematische Beziehungen
Das Dreiecksprisma folgt eleganten mathematischen Gesetzen mit √3:
Volumen-Formel
Basisfläche mal Höhe. Elegante √3-Formel.
Oberflächen-Formel
Zwei Dreiecke plus drei Rechtecke. Kombinierte Flächenformel.
Anwendungen des Dreiecksprismas
Dreiecksprismen finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Dachkonstruktionen
- Strukturelle Träger
- Moderne Gebäudeelemente
- Brückenkonstruktionen
Wissenschaft & Technik
- Optische Prismen
- Kristallstrukturen
- Mechanische Bauteile
- Geometrische Studien
Bildung & Lehre
- Geometrie-Unterricht
- Volumen-Berechnungen
- 3D-Geometrie Grundlagen
- Prisma-Mathematik
Design & Kunst
- Skulpturale Formen
- Dekorative Objekte
- Moderne Kunst
- Geometrische Muster
Formeln zum regelmäßigen Dreiecksprisma
Basisfläche (A)
Fläche des gleichseitigen Dreiecks
Volumen (V)
Basisfläche mal Höhe
Oberfläche (S)
Zwei Dreiecke plus drei Rechtecke
Höhe (h)
Höhe aus Volumen berechnen
Dreiecksprisma Parameter
2 gleichseitige Dreiecke
3 Rechtecke
9 Kanten total
3-fach rotational
Alle Formeln basieren auf der Seitenlänge a und der Höhe h
Berechnungsbeispiel für ein Dreiecksprisma
Gegeben
Gesucht: Volumen und Oberfläche des Dreiecksprismas
1. Basisflächen-Berechnung
Die Basisfläche beträgt 10.825 Flächeneinheiten
2. Volumen-Berechnung
Das Volumen beträgt 86.6 Volumeneinheiten
3. Oberflächen-Berechnung
Die Oberfläche beträgt 141.65 Flächeneinheiten
4. Aufschlüsselung
2 Dreiecke: 2 × 10.825 = 21.65
3 Rechtecke: 3 × 5 × 8 = 120
Gesamt: 21.65 + 120 = 141.65
Aufschlüsselung der Oberflächenberechnung
5. Das regelmäßige Dreiecksprisma
Das regelmäßige Dreiecksprisma mit perfekter dreieckiger Symmetrie
Das Dreiecksprisma: Eleganz der Dreiecksgeometrie
Das regelmäßige Dreiecksprima ist ein außergewöhnlicher geometrischer Körper, der die Eleganz der Dreiecksgeometrie in dreidimensionaler Form verkörpert. Mit seinen zwei kongruenten gleichseitigen Dreiecken als Grund- und Deckfläche und drei rechteckigen Seitenflächen stellt es eine perfekte Synthese aus Einfachheit und mathematischer Schönheit dar. Die charakteristische Verwendung der Wurzel aus 3 in allen Berechnungen verbindet es direkt mit den fundamentalen Eigenschaften des gleichseitigen Dreiecks und macht es zu einem idealen Studienobjekt für das Verständnis prismatischer Geometrie.
Die Geometrie des gleichseitigen Dreiecks
Das Dreiecksprisma verkörpert die Perfektion der Dreiecksgeometrie:
- Gleichseitige Basis: Alle Seiten der Grundfläche gleich lang
- Wurzel-3-Mathematik: √3 erscheint in allen Flächenberechnungen
- Prismatische Form: Parallelität zwischen Grund- und Deckfläche
- Rechteckige Seiten: Drei kongruente rechteckige Seitenflächen
- Dreifache Symmetrie: Rotationssymmetrie um die Höhenachse
- Euler-Charakteristik: V - E + F = 6 - 9 + 5 = 2
- Einfache Berechnung: Klare mathematische Beziehungen
Praktische Bedeutung und Anwendungen
Strukturelle Effizienz
Das Dreiecksprisma bietet eine optimale Balance zwischen Materialverbrauch und struktureller Stabilität, was es für Architektur und Ingenieurswesen wertvoll macht.
Optische Anwendungen
Als optisches Prisma nutzt es die Eigenschaft der Lichtbrechung und Dispersion, wobei die dreieckige Form optimale optische Eigenschaften bietet.
Pädagogischer Wert
Seine einfachen, aber eleganten mathematischen Beziehungen machen es zu einem idealen Lehrobjekt für die Einführung in die 3D-Geometrie und Volumenberechnungen.
Architektonische Ästhetik
Die markante Form des Dreiecksprismas wird in der modernen Architektur für dynamische und zugleich stabile Konstruktionen geschätzt.
Zusammenfassung
Das regelmäßige Dreiecksprisma steht als perfektes Beispiel für die Harmonie zwischen geometrischer Einfachheit und praktischer Anwendbarkeit. Seine mathematischen Beziehungen, durchdrungen von der Eleganz der Wurzel aus 3, machen es zu einem fundamentalen Baustein des geometrischen Verständnisses. Von seiner Rolle in optischen Instrumenten bis zu seinen Anwendungen in Architektur und Ingenieurswesen zeigt das Dreiecksprisma, wie grundlegende geometrische Formen zu praktischen Lösungen und ästhetischen Meisterwerken führen können. Als Brücke zwischen der zweidimensionalen Dreiecksgeometrie und der dreidimensionalen Raumgeometrie bleibt es ein unverzichtbares Element der mathematischen Bildung und praktischen Anwendung.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder