Schiefes Prisma berechnen
Rechner und Formeln zur Berechnung eines schiefen Prisma
Schiefes Prisma Rechner
Das schiefe Prisma
Bei einem schiefen Prisma ist die Deckfläche horizontal verschoben. Die Seiten bestehen aus Parallelogrammen.
Schiefes Prisma Eigenschaften
Das schiefe Prisma: Grundfläche und Deckfläche sind parallel aber horizontal verschoben
Schiefes Prisma Struktur
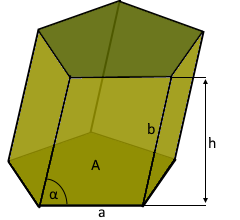
Das schiefe Prisma mit verschobener Deckfläche.
Parallelogramm-Seitenflächen verbinden Basis und Deckfläche.

|
|
Was ist ein schiefes Prisma?
Ein schiefes Prisma ist ein besonderer geometrischer Körper:
- Definition: Prisma mit horizontal verschobener Deckfläche zur Grundfläche
- Grundfläche: Beliebiges n-Eck (meist regelmäßig)
- Seitenflächen: Parallelogramme statt Rechtecke
- Winkel α: Neigungswinkel zwischen Basis und Seitenfläche
- Höhe h: Senkrechter Abstand zwischen Grund- und Deckfläche
- Länge b: Seitenlänge der Parallelogramm-Flächen
Geometrische Eigenschaften des schiefen Prismas
Das schiefe Prisma zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Eckenanzahl (n): Bestimmt die Form der Grundfläche
- Seitenlänge (a): Kantenlänge der Grundfläche
- Höhe (h): Senkrechter Abstand zwischen den Flächen
- Winkel (α): Neigungswinkel der Seitenflächen
Besondere Eigenschaften
- Parallelogramm-Seiten: Alle Seitenflächen sind Parallelogramme
- Verschiebung: Deckfläche ist zur Grundfläche versetzt
- Volumenerhaltung: Gleiches Volumen wie gerades Prisma
- Flexibilität: Verschiedene Neigungswinkel möglich
Mathematische Beziehungen
Das schiefe Prisma folgt klaren mathematischen Gesetzmäßigkeiten:
Volumen Formel
Das Volumen ist das Produkt aus Grundfläche und Höhe. Unabhängig vom Neigungswinkel.
Oberfläche Formel
Summe aus beiden Grundflächen plus n Parallelogramm-Seitenflächen.
Anwendungen des schiefen Prismas
Schiefe Prismen finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Geneigte Gebäudeteile und Dächer
- Trapezförmige Bauwerke
- Brückenkonstruktionen
- Moderne Architekturformen
Technik & Industrie
- Maschinenbauteile mit Neigung
- Optische Prismen und Linsen
- Behälter mit geneigten Wänden
- Designelemente in der Fertigung
Bildung & Lehre
- Geometrieunterricht und Demonstrationen
- Raumvorstellungsübungen
- Mathematische Modellierung
- Trigonometrie-Beispiele
Naturwissenschaften
- Kristallografie und Mineralogie
- Optik und Lichtbrechung
- Volumenberechnungen in der Chemie
- Physikalische Modellierungen
Formeln für das schiefe Prisma
Basisfläche A
Grundfläche eines regelmäßigen n-Ecks
Oberfläche S
Zwei Grundflächen plus n Seitenflächen
Höhe h
Aus Seitenlänge b und Winkel α
Länge b
Aus Höhe h und Winkel α
Volumen V
Grundfläche mal Höhe - unabhängig von der Neigung
Berechnungsbeispiel für ein schiefes Prisma
Gegeben
Gesucht: Alle Eigenschaften des schiefen Prismas
1. Basisfläche berechnen
Die Basisfläche beträgt etwa 61.94 Flächeneinheiten
2. Seitenlänge b berechnen
Die Seitenlänge b beträgt etwa 10.35 Längeneinheiten
3. Volumen berechnen
Das Volumen beträgt etwa 619.4 Volumeneinheiten
4. Oberfläche berechnen
Die Oberfläche beträgt etwa 423.88 Flächeneinheiten
5. Zusammenfassung der Ergebnisse
Das schiefe Prisma mit verschobener Deckfläche und charakteristischen Eigenschaften
Das schiefe Prisma: Die Kunst der geneigten Geometrie
Das schiefe Prisma ist eine faszinierende Erweiterung des klassischen geraden Prismas. Durch die horizontale Verschiebung der Deckfläche zur Grundfläche entsteht eine elegante geometrische Form, die trotz ihrer Neigung viele der grundlegenden Eigenschaften des Prismas beibehält. Besonders bemerkenswert ist, dass das Volumen unverändert bleibt, während sich die Oberflächeneigenschaften durch die charakteristischen Parallelogramm-Seitenflächen verändern.
Die Geometrie der Parallelogramm-Seitenflächen
Das schiefe Prisma fasziniert durch seine einzigartigen Seiteneigenschaften:
- Parallelogramm-Struktur: Alle Seitenflächen sind Parallelogramme statt Rechtecke
- Konstante Kantenlängen: Die Grundkanten a bleiben unverändert zur geraden Form
- Variable Seitenlänge b: Abhängig vom Neigungswinkel α und der Höhe h
- Winkelbeziehungen: Der Winkel α bestimmt die Neigung der Seitenflächen
- Flächenerhaltung: Die Grundfläche bleibt in Form und Größe erhalten
- Verschiebungsvektor: Die Deckfläche ist um einen Vektor zur Grundfläche versetzt
- Symmetrieeigenschaften: Translationssymmetrie entlang der Prismenachse
Prismengeometrie und Transformation
Grundlegende Transformation
Aus einem geraden Prisma entsteht durch Scherung (Parallelverschiebung der Deckfläche) das schiefe Prisma. Diese Transformation erhält das Volumen, verändert aber die Oberflächeneigenschaften.
Invariante Eigenschaften
Volumen, Grundfläche und Höhe bleiben erhalten. Die Querschnitte parallel zur Grundfläche sind alle kongruent zur ursprünglichen Grundfläche.
Variable Eigenschaften
Oberfläche, Seitenlängen der Parallelogramme und die Winkel der Seitenflächen ändern sich mit dem Neigungswinkel α. Die Seitenflächen werden zu Parallelogrammen.
Trigonometrische Beziehungen
Die Beziehung h = b·sin(α) verbindet Höhe, Seitenlänge und Neigungswinkel. Diese fundamentale Beziehung ermöglicht alle weiteren Berechnungen.
Mathematische Prinzipien der Scherung
Das schiefe Prisma demonstriert wichtige mathematische Konzepte:
Cavalieri-Prinzip
Das Volumen bleibt bei der Scherung konstant, da alle Querschnitte parallel zur Grundfläche gleich bleiben. Dies illustriert das berühmte Cavalieri-Prinzip der Geometrie.
Affine Transformation
Die Transformation vom geraden zum schiefen Prisma ist eine affine Abbildung, die Parallelität und Verhältnisse erhält, aber Winkel und Abstände verändert.
Trigonometrische Anwendungen
Die Winkelbeziehungen im schiefen Prisma bieten praktische Anwendungen der Trigonometrie, insbesondere bei der Berechnung von Höhen und Seitenlängen.
Vektorielle Betrachtung
Das schiefe Prisma kann als Verschiebung der Grundfläche entlang eines Vektors verstanden werden, was wichtige Konzepte der Vektorgeometrie veranschaulicht.
Praktische Bedeutung und Anwendungen
Das schiefe Prisma findet vielfältige praktische Anwendungen:
- Architektur: Geneigte Gebäudeteile, schräge Wände, moderne Designelemente
- Maschinenbau: Keilförmige Bauteile, geneigte Führungen, Schrägschnitte
- Optik: Prismatische Bauteile, Lichtbrechung, optische Instrumente
- Bauwesen: Böschungen, Rampen, schräge Stützmauern
- Verpackungsindustrie: Optimierte Behälterformen, Materialeinsparung
- Kristallografie: Natürliche Kristallformen, Mineralstrukturen
- Lehre: Demonstration von Transformationen, Volumenerhaltung
Konstruktion und technische Herausforderungen
Präzisionsanforderungen
Die Herstellung schiefer Prismen erfordert präzise Winkeleinstellungen und exakte Parallelität der Grund- und Deckfläche. Kleinste Abweichungen können die geometrischen Eigenschaften beeinträchtigen.
Materialüberlegungen
Bei der Materialauswahl müssen die durch die Scherung entstehenden Spannungen berücksichtigt werden. Die Parallelogramm-Seitenflächen können unterschiedliche Belastungen erfahren.
Fertigungstechniken
Moderne CNC-Fertigung und 3D-Druck ermöglichen präzise Herstellung schiefer Prismen. Die Programmierung muss die komplexen Winkelbeziehungen berücksichtigen.
Qualitätskontrolle
Die Überprüfung der geometrischen Korrektheit erfordert spezialisierte Messverfahren, da herkömmliche rechtwinklige Messmethoden nicht anwendbar sind.
Pädagogische und didaktische Aspekte
Konzeptverständnis
Das schiefe Prisma eignet sich hervorragend zur Demonstration von Volumenerhaltung bei Formveränderung. Es zeigt, wie sich geometrische Eigenschaften bei Transformationen verhalten.
Trigonometrie-Anwendung
Die Winkelbeziehungen bieten praktische Übungen für trigonometrische Funktionen und deren Anwendung in realen geometrischen Problemen.
Raumvorstellung
Die Visualisierung schiefer Prismen fördert das räumliche Vorstellungsvermögen und hilft beim Verständnis dreidimensionaler Transformationen.
Problemlösungsstrategien
Die Berechnung schiefer Prismen erfordert systematisches Vorgehen und die Anwendung verschiedener geometrischer Prinzipien, was analytisches Denken fördert.
Zusammenfassung
Das schiefe Prisma stellt eine elegante Erweiterung der klassischen Prismengeometrie dar. Durch die Parallelverschiebung der Deckfläche entstehen charakteristische Parallelogramm-Seitenflächen, die trotz der Formveränderung das Volumen erhalten. Von der theoretischen Demonstration wichtiger geometrischer Prinzipien wie dem Cavalieri-Prinzip bis hin zu praktischen Anwendungen in Architektur und Technik zeigt das schiefe Prisma die Vielseitigkeit mathematischer Konzepte. Als Brücke zwischen einfacher Prismengeometrie und komplexeren räumlichen Transformationen bleibt es ein faszinierendes Studienobjekt für alle, die sich für die Schönheit und Anwendbarkeit der Geometrie interessieren.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder