Tetraeder Rechner
Onlinerechner und Formeln zur Berechnung eines regelmäßigen Tetraeders
Tetraeder Rechner
Das Tetraeder
Das Tetraeder ist der einfachste platonische Körper mit 4 gleichseitigen Dreiecken und √2, √3, √6-Beziehungen.
Platonischer Körper Eigenschaften
Der einfachste Körper: 4 gleichseitige Dreiecke mit √2, √3, √6-Proportionen
Tetraeder Struktur
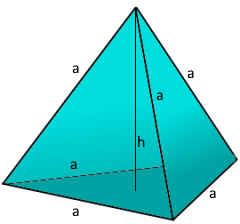
Der einfachste platonische Körper.
4 gleichseitige Dreiecke.
|
|
Was ist ein Tetraeder?
Das Tetraeder ist der einfachste der fünf platonischen Körper:
- Definition: Körper mit 4 gleichseitigen Dreiecken
- Platonischer Körper: Der einfachste der fünf regulären Polyeder
- Flächen: 4 kongruente gleichseitige Dreiecke
- Ecken: 4 Ecken insgesamt
- Kanten: 6 Kanten (alle gleich lang)
- Selbst-dual: Dual zu sich selbst
Geometrische Eigenschaften des Tetraeders
Das Tetraeder zeigt die Reinheit der minimalen 3D-Struktur:
Grundparameter
- Flächen: 4 gleichseitige Dreiecke
- Ecken: 4 Ecken
- Kanten: 6 Kanten (alle gleich lang)
- Euler-Charakteristik: V - E + F = 4 - 6 + 4 = 2
Besondere Eigenschaften
- Simplex: Einfachste 3D-Form
- Selbst-dual: Dual zu sich selbst
- Platonisch: Ursprung aller Polyeder
- Minimale Struktur: Kleinste konvexe 3D-Form
Mathematische Beziehungen
Das Tetraeder folgt den elementaren Wurzel-Gesetzen:
Volumen-Formel
Enthält die Quadratwurzel von 2. Einfach und fundamental.
Oberflächen-Formel
4 gleichseitige Dreiecke. Reine √3 Beziehung.
Anwendungen des Tetraeders
Tetraeder finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Raumfachwerke
- Strukturelle Grundelemente
- Minimale Rahmenstrukturen
- Spannungsverteilung
Wissenschaft & Technik
- Molekulare Geometrie
- Koordinationschemie
- Nanostrukturen
- Computergrafik (Triangulation)
Bildung & Lehre
- Geometrie-Grundlagen
- Einführung in 3D-Formen
- Platonische Körper
- Räumliches Vorstellungsvermögen
Kunst & Design
- Minimalistische Skulpturen
- Moderne Kunstwerke
- Spielwürfel (W4)
- Geometrische Objekte
Formeln zur Berechnung eines Tetraeders
Volumen (V)
Volumen mit der Quadratwurzel von 2
Oberfläche (S)
4 gleichseitige Dreiecke
Höhe (h)
Höhe mit √6
Umkugelradius (R)
Radius der Umkugel
Inkugelradius (r)
Radius der Inkugel
Kantenlänge zu Höhe
Verhältnis Höhe zur Kantenlänge
Die Wurzel-Proportionen des Tetraeders
√2 ≈ 1.414
√3 ≈ 1.732
√6 ≈ 2.449
Das Tetraeder vereint die grundlegenden Quadratwurzeln der Geometrie
Berechnungsbeispiel für ein Tetraeder
Gegeben
Gesucht: Alle Eigenschaften des Tetraeders
1. Volumen-Berechnung
Für a = 10:
\[V = \frac{10^3 \sqrt{2}}{12}\] \[V ≈ \frac{1000 \cdot 1.414}{12}\] \[V ≈ 117.9\]Das Volumen beträgt etwa 118 Volumeneinheiten
2. Oberflächen-Berechnung
Für a = 10:
\[S = 10^2 \sqrt{3}\] \[S ≈ 100 \cdot 1.732\] \[S ≈ 173.2\]Die Oberfläche beträgt etwa 173 Flächeneinheiten
3. Höhen-Berechnung
Für a = 10:
\[h = \frac{10 \sqrt{6}}{3}\] \[h ≈ \frac{10 \cdot 2.449}{3}\] \[h ≈ 8.16\]Die Höhe beträgt etwa 8.16 Längeneinheiten
4. Das perfekte Tetraeder
Das Tetraeder mit perfekter Wurzel-Harmonie
Das Tetraeder: Der einfachste Platonische Körper
Das Tetraeder ist der fundamentalste aller platonischen Körper und verkörpert die Reinheit der minimalen 3D-Struktur. Mit seinen nur 4 gleichseitigen Dreiecken, 4 Ecken und 6 Kanten ist es der einfachste mögliche konvexe Polyeder im dreidimensionalen Raum. Seine mathematische Eleganz zeigt sich in den grundlegenden Wurzel-Beziehungen: √2 im Volumen, √3 in der Oberfläche und √6 in der Höhe. Als einziger selbst-dualer platonischer Körper demonstriert es die perfekte Symmetrie zwischen Innen- und Außenstruktur.
Die Reinheit der minimalen 3D-Struktur
Das Tetraeder zeigt die fundamentalen Prinzipien der dreidimensionalen Geometrie:
- Simplex: Die einfachste mögliche 3D-Form
- Wurzel-Harmonie: Vereint √2, √3 und √6 in eleganter Weise
- Selbst-dual: Einziger platonischer Körper, der zu sich selbst dual ist
- Minimale Struktur: Kleinste Anzahl von Flächen für einen 3D-Körper
- Grundform: Basis für komplexere geometrische Strukturen
- Triangulation: Grundelement der 3D-Computergrafik
- Strukturelle Effizienz: Optimale Stabilität bei minimaler Masse
Mathematische Grundlagen
Wurzel-Vereinigung
Das Tetraeder ist der einzige platonische Körper, der die drei grundlegenden Quadratwurzeln √2, √3 und √6 in einer Form vereint.
Geometrische Einfachheit
Mit nur 4 Dreiecken, 4 Ecken und 6 Kanten ist es die minimale Struktur für einen dreidimensionalen Körper.
Selbst-Dualität
Als einziger selbst-dualer platonischer Körper zeigt es perfekte innere Symmetrie.
Fundamentale Bedeutung
Das Tetraeder ist die Grundlage für das Verständnis aller komplexeren 3D-Geometrien.
Zusammenfassung
Das Tetraeder verkörpert die Essenz der dreidimensionalen Geometrie und steht als fundamentale Grundform aller platonischen Körper da. Seine Struktur aus nur 4 gleichseitigen Dreiecken, durchdrungen von den Quadratwurzeln 2, 3 und 6, macht es zu einem faszinierenden Studienobjekt für Mathematiker, Ingenieure und Künstler. Von der molekularen Chemie über strukturelle Anwendungen bis hin zur Computergrafik zeigt das Tetraeder, wie geometrische Einfachheit und strukturelle Effizienz Hand in Hand gehen. Seine selbst-duale Natur und die Vereinigung der grundlegenden Wurzel-Konstanten machen es zu einem zeitlosen Symbol für die Macht der minimalen Komplexität. Als einfachster aller platonischen Körper bleibt das Tetraeder ein faszinierendes Beispiel für die Schönheit der mathematischen Klarheit und geometrischen Perfektion.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder