Pentagonales Trapezoeder Rechner
Rechner und Formeln zur Berechnung eines regelmäßigen pentagonalen Trapezoeder
Pentagonales Trapezoeder Rechner
Das Pentagonale Trapezoeder
Ein Pentagonales Trapezoeder ist eine verdrehte Doppelpyramide mit 10 deltoidalen Flächen im goldenen Schnitt.
Pentagonales Trapezoeder Struktur
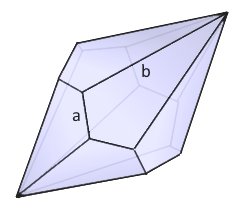
Die elegante verdrehte Doppelpyramide mit 10 Deltoidflächen.
Mathematische Perfektion im goldenen Schnitt.
|
|
Was ist ein Pentagonales Trapezoeder?
Ein Pentagonales Trapezoeder ist ein faszinierender dreidimensionaler Körper:
- Definition: Verdrehte Doppelpyramide mit pentagonaler Basis um 36°
- Flächen: 10 kongruente deltoidale (drachenförmige) Flächen
- Struktur: Zwei fünfeckige Pyramiden, um 180°/5 = 36° gegeneinander verdreht
- Ecken: 12 Ecken (2 Pol-Ecken + 10 Äquator-Ecken)
- Kanten: 20 Kanten in zwei verschiedenen Längen
- Symmetrie: Dihedrale Symmetriegruppe D5d
Geometrische Eigenschaften des Pentagonalen Trapezoeders
Das Pentagonale Trapezoeder zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Kantenlängen: Zwei verschiedene Kantenlängen a und b
- Flächen: 10 kongruente Deltoidflächen
- Euler-Charakteristik: V - E + F = 12 - 20 + 10 = 2
- Verdrehung: Obere Pyramide um 36° verdreht zur unteren
Besondere Eigenschaften
- Trapezoeder-Familie: Gehört zu den Trapezoeder-Polyedern
- Deltoidflächen: Jede Fläche ist ein symmetrisches Drachenviereck
- Goldener Schnitt: Alle Proportionen enthalten φ = (1+√5)/2
- Pentagonale Symmetrie: 5-zählige Rotationssymmetrie
Mathematische Beziehungen
Das Pentagonale Trapezoeder folgt eleganten mathematischen Gesetzen mit dem goldenen Schnitt:
Volumenformel
Basierend auf der Antiprisma-Länge z. Koeffizient enthält den goldenen Schnitt √5.
Oberflächenformel
Summe von 10 Deltoidflächen. Goldener Schnitt √5 in der Wurzel.
Anwendungen des Pentagonalen Trapezoeders
Pentagonale Trapezoeder finden Anwendung in verschiedenen Bereichen:
Wissenschaft & Forschung
- Kristallographie und Quasikritstall-Strukturen
- Molekülchemie mit pentagonaler Symmetrie
- Topologie und Polyeder-Theorie
- Goldener Schnitt in der Natur
Technik & Design
- 3D-Spielwürfel und Gaming-Komponenten
- Architektonische Gestaltungselemente
- CAD-Software und Geometrie-Algorithmen
- Optische Instrumente und Prismen
Bildung & Lehre
- Geometrie-Unterricht und Demonstrations-objekte
- Polyeder-Studien und Euler-Formel
- Symmetrie-Konzepte und Gruppentheorie
- Goldener Schnitt in der Mathematik
Kunst & Gestaltung
- Skulpturale Kunstwerke und Installationen
- Architektonische Ornamente und Muster
- Schmuck-Design mit geometrischen Formen
- Mathematische Kunst und Fraktale
Formeln für das Pentagonale Trapezoeder
Seitelänge a (goldener Schnitt)
Kurze Seite mit goldenem Schnitt φ⁻¹
Seitelänge b (goldener Schnitt)
Lange Seite mit goldenem Schnitt φ
Höhe h
Höhe mit verschachtelter √5-Formel
Oberfläche S
Oberfläche mit goldenem Schnitt √5
Volumen V
Volumen mit goldenem Schnitt (3 + √5)
Goldener Schnitt Konstanten
≈ 1.618034
≈ 0.618034
≈ 2.236068
≈ 3.077684
Alle Formeln basieren auf diesen irrationalen Konstanten
Berechnungsbeispiel für ein Pentagonales Trapezoeder
Gegeben
Gesucht: Alle Eigenschaften der verdrehten Doppelpyramide
1. Seitelängen berechnen
Kurze und lange Seite mit goldenem Schnitt
2. Höhe berechnen
Die Höhe der verdrehten Doppelpyramide
3. Oberfläche berechnen
Die Oberfläche aller 10 Deltoidflächen
4. Volumen berechnen
Das Volumen der verdrehten Doppelpyramide
5. Zusammenfassung der Ergebnisse
Ein perfektes Beispiel für den goldenen Schnitt in der Geometrie
Das Pentagonale Trapezoeder: Eleganz der verdrehten Doppelpyramide
Das Pentagonale Trapezoeder ist ein außergewöhnliches geometrisches Objekt, das die Eleganz der pentagonalen Symmetrie mit der Komplexität des goldenen Schnitts verbindet. Als verdrehte Doppelpyramide mit 10 deltoidalen Flächen repräsentiert es eine perfekte Balance zwischen mathematischer Präzision und ästhetischer Schönheit. Die charakteristische Verdrehung um 36° (180°/5) zwischen der oberen und unteren Pyramide erzeugt eine faszinierende Geometrie, die durch den goldenen Schnitt φ = (1+√5)/2 in allen Proportionen durchdrungen ist.
Die Geometrie der Verdrehung
Das Pentagonale Trapezoeder fasziniert durch seine einzigartige Konstruktion:
- Doppelpyramiden-Struktur: Zwei pentagonale Pyramiden, deren Grundflächen zusammengefügt sind
- 36°-Verdrehung: Die obere Pyramide ist um 180°/5 = 36° gegenüber der unteren verdreht
- 10 Deltoidflächen: Jede Fläche ist ein symmetrisches Drachenviereck mit zwei Paar gleichen Seiten
- Zwei Eckentypen: 2 Pol-Ecken (Spitzen) und 10 Äquator-Ecken am Übergang
- Drei Kantentypen: Polare Kanten, äquatoriale Kanten und laterale Kanten
- Goldener Schnitt: Alle Seitenverhältnisse basieren auf φ und φ⁻¹
- D5d-Symmetrie: Dihedrale Symmetriegruppe mit 5-zähliger Rotation und Spiegelung
Pentagonale Symmetrie und der goldene Schnitt
Pentagonale Grundlage
Das Pentagon ist untrennbar mit dem goldenen Schnitt verbunden. Jede pentagonale Struktur zeigt automatisch φ-Proportionen, was dieses Trapezoeder zu einem natürlichen Träger des goldenen Schnitts macht.
Fibonacci-Verbindung
Die Formeln enthalten √5-Terme, die direkt mit der Fibonacci-Folge zusammenhängen. Dies zeigt die tiefe Verbindung zwischen dieser Geometrie und natürlichen Wachstumsmustern.
Proportionsharmonie
Das Verhältnis der langen zur kurzen Deltoidseite beträgt exakt φ² ≈ 2.618, was zu den harmonischsten Proportionen in der Geometrie gehört und eine natürliche ästhetische Anziehung erzeugt.
Irrationale Schönheit
Obwohl alle Maße auf irrationalen Zahlen basieren, erzeugt diese "Ungenauigkeit" paradoxerweise eine perfekte mathematische und visuelle Harmonie.
Trapezoeder-Familie und mathematische Verwandtschaft
Das Pentagonale Trapezoeder gehört zur Familie der Trapezoeder:
Trapezoeder-Prinzip
Alle Trapezoeder entstehen durch Verdrehung zweier n-eckiger Pyramiden um 180°/n. Beim pentagonalen Fall ergibt sich die charakteristische 36°-Verdrehung, die optimal für den goldenen Schnitt ist.
Mathematische Verwandtschaft
Es steht in enger Beziehung zu anderen pentagonalen Körpern wie dem Dodekaeder und Ikosaeder, teilt aber nicht deren platonische Perfektion, sondern zeigt eine "gebrochene" Symmetrie.
Deltoid-Eigenschaften
Jede der 10 Deltoidflächen hat identische Innenwinkel und Seitenverhältnisse, wodurch eine perfekte Tessellation um die zentrale Achse entsteht. Dies ist nur durch die 36°-Verdrehung möglich.
Symmetrie-Bruch
Im Gegensatz zu den platonischen Körpern zeigt es "gebrochene" Symmetrie - perfekt strukturiert, aber nicht vollständig regular, was zu seiner besonderen ästhetischen Anziehung beiträgt.
Wissenschaftliche und kulturelle Bedeutung
Das Pentagonale Trapezoeder findet breite Anwendung und kulturelle Bedeutung:
- Quasikritstall-Forschung: Modell für pentagonale Quasi-periodische Strukturen
- Botanik: Verständnis pentagonaler Blütenstrukturen und Phyllotaxis
- Spieltheorie: Grundlage für 10-seitige Würfel (d10) in Rollenspielen
- Architektur: Inspiration für pentagonale Bauelemente und Ornamente
- Optik: Prismenformen für spezielle Lichtbrechungseffekte
- Molekularchemie: Template für pentagonale Molekülkäfige
- Kunstgeschichte: Symbol für Harmonie zwischen Ordnung und Chaos
Konstruktion und praktische Herausforderungen
Fertigungsgenauigkeit
Die Herstellung erfordert höchste Präzision bei der 36°-Verdrehung und den irrationalen Seitenlängen. Bereits kleine Abweichungen zerstören die charakteristische Deltoid-Form der Flächen.
CAD-Herausforderungen
Moderne CAD-Software muss mit den irrationalen √5-Termen umgehen können. Die Rundungsfehler akkumulieren schnell und können die geometrische Integrität beeinträchtigen.
Materialwissenschaft
Die Spannungsverteilung in den Deltoidflächen folgt komplexen Mustern, die bei der Materialauswahl für physische Modelle berücksichtigt werden müssen.
Qualitätskontrolle
Die Verifikation der korrekten Geometrie erfordert spezialisierte Messverfahren, da die charakteristischen Winkel und Proportionen nur mit hoher Präzision erkennbar sind.
Philosophische und ästhetische Dimensionen
Harmonie der Gegensätze
Das Pentagonale Trapezoeder verkörpert die Balance zwischen Regelmäßigkeit (identische Deltoide) und Irregularität (gebrochene Symmetrie), was es zu einem philosophischen Symbol für die Komplexität des Lebens macht.
Natürliche Ästhetik
Die auf dem goldenen Schnitt basierenden Proportionen verleihen diesem Körper eine natürliche Schönheit, die sowohl mathematisch begründet als auch intuitiv ansprechend ist.
Bildungswert
Als Demonstrationsobjekt für den goldenen Schnitt, pentagonale Symmetrie und komplexe Polyeder-Konstruktionen bietet es unvergleichliche didaktische Möglichkeiten.
Spirituelle Symbolik
In verschiedenen Kulturen wird das Pentagon mit Vollkommenheit und Harmonie assoziiert. Die Verdrehung symbolisiert Transformation und Entwicklung.
Moderne Anwendungen und Zukunftsperspektiven
Nanotechnologie
Pentagonale Trapezoeder-Strukturen werden in der Nanotechnologie als Template für selbstorganisierende Systeme und als Bausteine für komplexe Nanomaterialien erforscht.
Computergrafik
In der 3D-Modellierung und Virtual Reality dienen sie als Benchmark für Algorithmen zur Darstellung komplexer Geometrien mit hoher Symmetrie und irrationalen Proportionen.
Robotik
Die mechanischen Eigenschaften der Deltoidflächen inspirieren neue Ansätze für adaptive Robotergelenke und transformierbare Strukturen in der Robotik.
Biomimetik
Das Studium pentagonaler Trapezoeder-Strukturen in der Natur führt zu neuen biomimetischen Materialien und Konstruktionsprinzipien.
Zusammenfassung
Das Pentagonale Trapezoeder steht als faszinierendes Beispiel für die Eleganz mathematischer Strukturen da. Seine 10 deltoidalen Flächen, durchdrungen vom goldenen Schnitt und arrangiert in einer charakteristischen 36°-Verdrehung, machen es zu einem Meisterwerk der Geometrie. Von seiner natürlichen Verbindung zur Fibonacci-Folge bis zu seinen modernen Anwendungen in Nanotechnologie und Robotik zeigt es, wie fundamentale mathematische Prinzipien sowohl theoretische Schönheit als auch praktischen Nutzen haben können. Als Bindeglied zwischen der antiken Faszination für pentagonale Symmetrie und den modernen Herausforderungen der computational geometry bleibt es ein inspirierendes Objekt für Mathematiker, Wissenschaftler, Künstler und alle, die von der Macht der Geometrie zur Erschaffung harmonischer Formen begeistert sind.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder