Regelmäßiges Prisma Rechner
Rechner und Formeln zur Berechnung eines regelmäßigen Prisma
Regelmäßiges Prisma Rechner
Das Regelmäßige Prisma
Ein Regelmäßiges Prisma ist ein dreidimensionaler Körper mit kongruenten regulären Grundflächen und rechteckigen Seitenflächen.
Regelmäßiges Prisma Eigenschaften
Der vielseitige Grundkörper: n+2 Flächen, 2n Ecken, 3n Kanten
Regelmäßiges Prisma Struktur
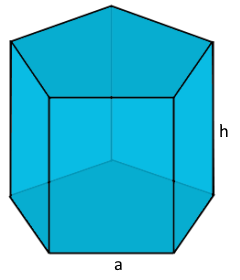
Der vielseitige Grundkörper mit regelmäßiger Grundfläche.
Konstante Querschnittsfläche über die gesamte Höhe.
|
|
Was ist ein Regelmäßiges Prisma?
Ein Regelmäßiges Prisma ist ein fundamentaler dreidimensionaler Körper:
- Definition: Körper mit zwei parallelen, kongruenten regulären Grundflächen
- Grundflächen: Regelmäßige n-Ecke (gleichseitige Dreiecke, Quadrate, etc.)
- Seitenflächen: Rechtecke, die die Grundflächen verbinden
- Flächen: n+2 Flächen (2 Grundflächen + n Seitenflächen)
- Ecken: 2n Ecken (n pro Grundfläche)
- Kanten: 3n Kanten (n pro Grundfläche + n Verbindungskanten)
Geometrische Eigenschaften des Regelmäßigen Prismas
Das Regelmäßige Prisma zeigt charakteristische geometrische Eigenschaften:
Grundparameter
- Grundfläche: Regelmäßiges n-Eck mit Seitenlänge a
- Höhe: Konstanter Abstand h zwischen den Grundflächen
- Euler-Charakteristik: V - E + F = 2n - 3n + (n+2) = 2
- Prisma-Achse: Senkrecht zu den Grundflächen
Besondere Eigenschaften
- Konstanter Querschnitt: Gleiche Grundfläche über gesamte Höhe
- Parallele Grundflächen: Obere und untere Fläche kongruent
- Rechteckige Seitenflächen: Alle Seitenflächen sind Rechtecke
- Translationssymmetrie: Verschiebung entlang der Prisma-Achse
Mathematische Beziehungen
Das Regelmäßige Prisma folgt eleganten mathematischen Gesetzen:
Volumenformel
Volumen = Grundfläche × Höhe. Einfachste aller Volumenformeln.
Oberflächenformel
Oberfläche = 2 Grundflächen + Mantelfläche. U = Umfang der Grundfläche.
Anwendungen des Regelmäßigen Prismas
Regelmäßige Prismen finden breite Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Säulen und Stützen mit polygonalen Querschnitten
- Dachkonstruktionen und Träger
- Moderne Hochhaus-Architektur
- Brückenelemente und Konstruktionsträger
Technik & Industrie
- Rohre und Leitungssysteme
- Maschinenbauteile und Profile
- Behälter und Tanks
- Präzisionswerkzeuge und Führungen
Wissenschaft & Forschung
- Kristallographie und Mineralstruktur-Analyse
- Optische Prismen und Lichtleitung
- Geometrie-Unterricht und Demonstrations-objekte
- 3D-Modellierung und CAD-Grundformen
Kunst & Design
- Skulpturale Installationen und Kunstwerke
- Möbeldesign und Innenarchitektur
- Schmuck und dekorative Objekte
- Verpackungsdesign und Produktgestaltung
Formeln für das Regelmäßige Prisma
Basisfläche A
Fläche des regelmäßigen n-Ecks
Volumen V
Grundfläche × Höhe
Höhe h
Höhe aus Volumen berechnen
Oberfläche S
2 Grundflächen + Mantelfläche
Häufige Grundflächen
A = (√3/4)·a²
A = a²
A ≈ 1.72·a²
A = (3√3/2)·a²
Verschiedene regelmäßige Grundflächen und ihre Flächenformeln
Wichtige Beziehungen
M = n·a·h
U = n·a
k = 1/(4·tan(π/n))
Hilfsformeln für die Prisma-Berechnungen
Berechnungsbeispiel für ein Regelmäßiges Prisma
Gegeben
Gesucht: Höhe h, Oberfläche S und Basisfläche A
1. Basisfläche berechnen
Die Grundfläche des Pentagons beträgt etwa 27.53 Flächeneinheiten
2. Höhe berechnen
Die Höhe des Prismas beträgt etwa 5.08 Längeneinheiten
3. Mantelfläche berechnen
Die Mantelfläche beträgt 101.6 Flächeneinheiten
4. Gesamtoberfläche berechnen
Die Gesamtoberfläche beträgt etwa 156.66 Flächeneinheiten
5. Zusammenfassung der Ergebnisse
Ein perfektes Beispiel für die Eleganz prismatischer Geometrie
Das Regelmäßige Prisma: Der vielseitige Grundkörper der Geometrie
Das Regelmäßige Prisma steht als einer der fundamentalsten und vielseitigsten Körper der dreidimensionalen Geometrie da. Seine elegante Struktur mit zwei parallelen, kongruenten regelmäßigen Grundflächen und rechteckigen Seitenflächen macht es zu einem unverzichtbaren Baustein in Mathematik, Technik und Architektur. Von den einfachen dreiseitigen Prismen bis zu den komplexeren vieleckigen Varianten verkörpert es das Prinzip der konstanten Querschnittsfläche und bildet die Grundlage für unzählige praktische Anwendungen.
Die Geometrie der konstanten Querschnitte
Das Regelmäßige Prisma fasziniert durch seine strukturelle Klarheit:
- Parallelität der Grundflächen: Zwei identische regelmäßige n-Ecke in parallelen Ebenen
- Konstanter Querschnitt: Jeder Schnitt parallel zu den Grundflächen ergibt dieselbe Form
- Rechteckige Seitenflächen: n Rechtecke verbinden die entsprechenden Kanten der Grundflächen
- Senkrechte Prisma-Achse: Die Verbindungslinie zwischen den Grundflächenzentren steht senkrecht
- Translationssymmetrie: Verschiebung entlang der Prisma-Achse ändert die Form nicht
- n-zählige Rotationssymmetrie: Drehung um 360°/n um die Prisma-Achse
- Spiegelsymmetrien: n Spiegelebenen durch die Prisma-Achse
Vielfalt der Grundflächen und ihre Eigenschaften
Einfache Grundflächen
Das Dreiecksprisma (n=3) mit gleichseitigen Dreiecken ist das einfachste regelmäßige Prisma. Das Quadratprisma (n=4) entspricht einem Quader mit quadratischer Grundfläche. Beide zeigen bereits alle charakteristischen Prisma-Eigenschaften.
Komplexere Formen
Pentagon- (n=5) und Hexagon-Prismen (n=6) zeigen interessante Symmetrien. Das Hexagon-Prisma ist besonders in der Natur zu finden (Bienenwaben, Basaltsäulen). Mit steigendem n nähert sich die Grundfläche einem Kreis an.
Mathematische Progression
Mit steigender Eckenzahl n wird tan(π/n) kleiner, wodurch die Grundfläche bei konstanter Seitenlänge größer wird. Der Grenzfall n→∞ führt zum Kreiszylinder mit A = πr² und U = 2πr.
Optimierungsaspekte
Für gegebenen Umfang maximiert das Hexagon die Fläche unter allen regelmäßigen Polygonen (Isoperimetrisches Problem), was seine Häufigkeit in der Natur erklärt.
Mathematische Eleganz und Formelstruktur
Das Regelmäßige Prisma zeigt bemerkenswerte mathematische Schönheit:
Trigonometrische Grundlage
Die Grundflächenformel A = na²/(4tan(π/n)) basiert auf der Zerlegung des n-Ecks in gleichschenklige Dreiecke. Der Tangens des halben Zentriwinkels bestimmt die Proportionen.
Volumenprinzip
Das Volumen V = A×h folgt dem fundamentalen Prinzip von Cavalieri: Körper mit gleichen Querschnittsflächen in allen Höhen haben gleiches Volumen.
Oberflächenzerlegung
Die Oberfläche S = 2A + U×h addiert zwei Grundflächen und die Mantelfläche. Dies zeigt die modulare Struktur des Prismas.
Skalierungsgesetze
Bei Skalierung um Faktor k ändern sich Längen mit k¹, Flächen mit k² und Volumen mit k³. Dies folgt den allgemeinen Dimensionsgesetzen.
Wissenschaftliche und technische Bedeutung
Das Regelmäßige Prisma findet breite wissenschaftliche und technische Anwendung:
- Baustatik: Träger mit polygonalen Querschnitten für optimale Materialverteilung
- Strömungsmechanik: Kanäle und Rohre mit nicht-kreisförmigen Querschnitten
- Optik: Prismen zur Lichtbrechung und Spektralzerlegung
- Kristallographie: Viele Kristalle wachsen in prismatischen Formen
- Materialwissenschaft: Faserstrukturen und Verbundwerkstoffe
- Robotik: Bewegungsführungen und mechanische Komponenten
- Verfahrenstechnik: Reaktoren und Behälter mit optimierten Querschnitten
Konstruktion und Fertigungstechnische Aspekte
Fertigungsvorteile
Regelmäßige Prismen sind einfach zu fertigen, da alle Seitenflächen identische Rechtecke sind. Dies reduziert Werkzeugkosten und Komplexität in der Produktion.
Materialeffizienz
Die klare Geometrie ermöglicht optimale Materialausnutzung und minimiert Verschnitt. Die Stapelbarkeit reduziert Transportkosten.
Verbindungstechnik
Die rechteckigen Seitenflächen ermöglichen einfache Verbindungen durch Schrauben, Schweißen oder Klemmen. Standardisierte Anschlüsse sind möglich.
Qualitätskontrolle
Die regelmäßige Geometrie erleichtert Messungen und Qualitätsprüfungen. Abweichungen von der Sollform sind leicht erkennbar.
Historische Entwicklung und kulturelle Bedeutung
Antike Ursprünge
Prismatische Formen finden sich bereits in der antiken Architektur. Griechische und römische Säulen zeigen oft polygonale Querschnitte. Die mathematische Theorie entwickelten Euklid und Archimedes.
Moderne Architektur
Im 20. Jahrhundert revolutionierten prismatische Hochhäuser die Stadtbilder. Die klare Geometrie entspricht den Idealen der Moderne: "Form follows function".
Industrialisierung
Die Massenproduktion machte prismatische Profile zu Standardbauteilen. Aluminium-Strangpressprofile ermöglichen komplexe, aber fertigungsgerechte Querschnitte.
Digitales Zeitalter
CAD-Software und 3D-Druck haben die Konstruktion komplexer prismatischer Formen demokratisiert. Parametrische Designs ermöglichen neue Gestaltungsfreiheiten.
Zukunftsperspektiven und Innovation
Smart Materials
Adaptive Prismen mit veränderbaren Querschnitten durch formgedächtnislegierungen oder piezoelektrische Aktoren eröffnen neue Anwendungsfelder in der Robotik und Luftfahrt.
Nachhaltigkeit
Optimierte prismatische Strukturen können Materialverbrauch reduzieren und Energieeffizienz steigern. Leichtbauweise bei hoher Stabilität wird zunehmend wichtiger.
Biomimetik
Die Natur zeigt optimierte prismatische Strukturen (Bambushalme, Knochen). Diese Vorbilder inspirieren neue technische Lösungen mit hervorragenden Materialeigenschaften.
Nanotechnologie
Prismatische Nanostrukturen finden Anwendung in der Photovoltaik, Katalyse und Sensorik. Die kontrollierte Geometrie auf Nanoskala ermöglicht maßgeschneiderte Eigenschaften.
Zusammenfassung
Das Regelmäßige Prisma steht als fundamentaler Baustein der dreidimensionalen Geometrie da. Seine Eleganz liegt in der Verbindung von mathematischer Klarheit mit praktischer Vielseitigkeit. Von den einfachen trigonometrischen Formeln für die Grundfläche bis zu den komplexen Anwendungen in Nanotechnologie und Biomimetik zeigt es, wie grundlegende geometrische Prinzipien über Jahrtausende hinweg relevant bleiben. Als Bindeglied zwischen der reinen Mathematik und den praktischen Herausforderungen von Technik und Architektur bleibt das Regelmäßige Prisma ein unverzichtbares Werkzeug für Ingenieure, Architekten, Wissenschaftler und alle, die die Macht der Geometrie zur Lösung realer Probleme nutzen wollen.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder