Geraden Keil berechnen
Rechner und Formeln zur Berechnung eines geraden Keils
Gerader Keil Rechner
Der Gerade Keil
Ein Gerader Keil ist ein Prisma mit dreieckiger Grundfläche und rechteckigen Seitenflächen.
Gerader Keil Eigenschaften
Der Keilkörper: Prisma mit dreieckiger Grundfläche
Gerader Keil Struktur
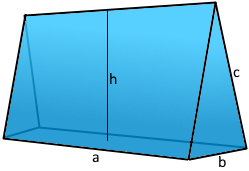
Der faszinierende Keilkörper mit dreieckiger Grundfläche.
Prismatische Form mit rechteckigen Seitenflächen.
|
|
Was ist ein Gerader Keil?
Ein Gerader Keil ist ein fundamentaler geometrischer Körper:
- Definition: Prisma mit rechtwinkliger dreieckiger Grundfläche
- Grundfläche: Rechtwinkliges Dreieck mit Katheten a und b
- Seitenflächen: Drei rechteckige Flächen
- Ecken: 6 Eckpunkte
- Kanten: 9 Kanten (6 Grundkanten + 3 Höhenkanten)
- Symmetrie: Spiegelsymmetrie bezüglich einer Ebene
Geometrische Eigenschaften des geraden Keils
Der Gerade Keil zeigt charakteristische geometrische Eigenschaften:
Grundparameter
- Katheten: Zwei senkrechte Seiten a und b
- Hypotenuse: Schräge Seite c der Grundfläche
- Höhe: Senkrechte Ausdehnung h des Prismas
- Euler-Charakteristik: V - E + F = 6 - 9 + 5 = 2
Besondere Eigenschaften
- Rechtwinkligkeit: 90° Winkel zwischen Katheten
- Prismaform: Gleichmäßige Höhe über gesamte Grundfläche
- Pythagoras: c² = a² + b² für Grundfläche
- Einfache Berechnung: Grundlegende geometrische Formeln
Mathematische Beziehungen
Der Gerade Keil folgt einfachen aber fundamentalen mathematischen Gesetzmäßigkeiten:
Volumenformel
Grundfläche mal Höhe durch zwei. Hälfte eines entsprechenden Quaders.
Oberflächenformel
Summe aller Einzelflächen. Grund- plus drei Seitenflächen.
Anwendungen des geraden Keils
Gerade Keile finden in zahlreichen praktischen Bereichen Anwendung:
Technik & Industrie
- Maschinenbau und Werkzeugherstellung
- Spannvorrichtungen und mechanische Keile
- Dachkonstruktionen und Bauingenieurwesen
- Verpackungsdesign und Logistik
Wissenschaft & Technik
- 3D-Modellierung und CAD-Software
- Finite-Elemente-Methoden
- Optische Prismen und Lichtleitung
- Akustische Anwendungen
Bildung & Lehre
- Geometrieunterricht und Grundlagen
- Volumen- und Oberflächenberechnungen
- Prisma-Studien und räumliche Geometrie
- Räumliches Vorstellungsvermögen
Alltag & Architektur
- Architektonische Gestaltungselemente
- Möbeldesign und Innenarchitektur
- Landschaftsarchitektur
- Kunstobjekte und Skulpturen
Formeln zum geraden Keil
Volumen V
Volumen des Keilkörpers - halbes Quadervolumen
Gesamtoberfläche S
Summe aller Einzelflächen des Keils
Seitenlänge c
Schräge Seitenlänge mit Pythagoras
Höhe h
Höhe des Keilkörpers aus Hypotenuse
Grundflächen-Eigenschaften
\[A_G = \frac{a \cdot b}{2}\]
\[U_G = a + b + \sqrt{a^2 + b^2}\]
\[c_G = \sqrt{a^2 + b^2}\]
Eigenschaften der rechtwinkligen dreieckigen Grundfläche
Seitenflächen-Bereiche
A₁ = a · h
A₂ = b · h
A₃ = c · h
Die drei rechteckigen Seitenflächen des Keils
Berechnungsbeispiel für einen geraden Keil
Gegeben
Gesucht: Alle Eigenschaften des Keilkörpers
1. Hypotenuse berechnen
Die Hypotenuse der Grundfläche beträgt etwa 11.18 Einheiten
2. Volumen berechnen
Das Volumen beträgt 100 Kubikeinheiten
3. Grundfläche berechnen
Die Grundfläche beträgt 25 Quadrateinheiten
4. Oberfläche berechnen
Die Gesamtoberfläche beträgt etwa 293.6 Quadrateinheiten
5. Seitenflächen im Detail
Der praktische Keilkörper mit klaren geometrischen Verhältnissen
Der Gerade Keil: Der praktische Grundkörper der Geometrie
Der Gerade Keil ist einer der fundamentalsten und praktischsten geometrischen Körper. Mit seiner rechtwinkligen dreieckigen Grundfläche und rechteckigen Seitenflächen verkörpert er eine perfekte Verbindung zwischen mathematischer Einfachheit und praktischer Anwendbarkeit. Als Prisma mit dreieckiger Grundfläche repräsentiert er grundlegende Prinzipien der räumlichen Geometrie, wo jede seiner Eigenschaften durch elementare mathematische Beziehungen beschrieben werden kann.
Die Geometrie der rechtwinkligen Grundfläche
Der Gerade Keil fasziniert durch seine klaren geometrischen Eigenschaften:
- Rechtwinklige Grundfläche: Dreieck mit zwei Katheten a und b sowie Hypotenuse c
- Pythagoras-Beziehung: c² = a² + b² für die Grundfläche
- Prismatische Form: Gleichmäßige Höhe h über der gesamten Grundfläche
- Rechteckige Seitenflächen: Drei Rechtecke mit Flächen a·h, b·h und c·h
- Einfache Formeln: Alle Berechnungen basieren auf elementaren geometrischen Gesetzen
- Praktische Anwendbarkeit: Ideale Form für technische und architektonische Anwendungen
- Symmetrieeigenschaften: Spiegelsymmetrie bezüglich der Ebene durch die Höhe und Hypotenuse
Prismen und räumliche Geometrie
Prisma-Prinzipien
Als Prisma mit dreieckiger Grundfläche folgt der Gerade Keil den allgemeinen Prisma-Gesetzmäßigkeiten: konstante Querschnittsfläche, parallele Grund- und Deckfläche, rechteckige Seitenflächen.
Rechtwinklige Geometrie
Die rechtwinklige Grundfläche macht alle Berechnungen besonders einfach und ermöglicht die direkte Anwendung des Satzes von Pythagoras sowie elementarer Flächenformeln.
Räumliche Erweiterung
Der Übergang von der zweidimensionalen Dreiecksfläche zum dreidimensionalen Keilkörper demonstriert fundamental die Prinzipien der räumlichen Geometrie.
Elementare Mathematik
Alle Formeln verwenden nur grundlegende arithmetische Operationen und Quadratwurzeln, was ihn ideal für Bildungszwecke und praktische Anwendungen macht.
Mathematische Einfachheit und Klarheit
Der Gerade Keil zeichnet sich durch mathematische Klarheit aus:
Einfache Formeln
Volumen = (a·b·h)/2 und Oberfläche = a·b + 2·a·c + h·b sind elementare Formeln, die ohne komplexe mathematische Kenntnisse anwendbar sind.
Pythagoras-Anwendung
Die Beziehung zwischen Katheten und Hypotenuse folgt direkt dem Satz des Pythagoras, einem der fundamentalsten Gesetze der Geometrie.
Praktische Berechenbarkeit
Alle Parameter lassen sich mit einfachen Mitteln berechnen, was den Keil ideal für praktische Anwendungen in Technik und Handwerk macht.
Didaktischer Wert
Als Einführung in die räumliche Geometrie bietet der Gerade Keil einen idealen Übergang von der Flächen- zur Körpergeometrie.
Praktische und technische Bedeutung
Der Gerade Keil findet weitreichende praktische Anwendungen:
- Maschinenbau: Keile als Spannelemente, Führungen und Verbindungselemente
- Bauwesen: Dachkonstruktionen, Fundamente und architektonische Elemente
- Optik: Prismen für Lichtlenkung und spektroskopische Anwendungen
- Verpackung: Effiziente Raumnutzung und stabile Konstruktionen
- Design: Ästhetische Gestaltungselemente in Architektur und Produktdesign
- Bildung: Grundlagenverständnis für räumliche Geometrie und Volumenberechnungen
- Simulation: Einfache Testobjekte für 3D-Modellierung und Finite-Elemente-Methoden
Herstellung und praktische Realisierung
Fertigungsfreundlichkeit
Die einfachen geometrischen Formen machen den Geraden Keil besonders fertigungsfreundlich. Alle Flächen sind eben und können mit konventionellen Werkzeugen bearbeitet werden.
Materialeffizienz
Die klaren geometrischen Verhältnisse ermöglichen optimale Materialausnutzung und minimalen Verschnitt bei der Herstellung.
Qualitätskontrolle
Die einfachen Maße und rechtwinkligen Verhältnisse ermöglichen unkomplizierte Qualitätskontrolle mit Standardmesswerkzeugen.
Vielseitigkeit
Durch Variation der Parameter a, b und h lässt sich eine große Vielfalt an Keilformen für unterschiedlichste Anwendungen realisieren.
Pädagogische und wissenschaftliche Aspekte
Bildungswert
Der Gerade Keil eignet sich ideal für den Geometrieunterricht, da er grundlegende Konzepte wie Fläche, Volumen und räumliche Beziehungen auf einfache Weise vermittelt.
Anschaulichkeit
Die klaren, rechtwinkligen Strukturen sind leicht vorstellbar und können mit einfachen Mitteln als Modelle hergestellt werden.
Wissenschaftliche Relevanz
In der numerischen Mathematik dienen Keilformen als Grundelemente für komplexere Berechnungsverfahren und finite Elemente.
Transferwert
Die am Geraden Keil erlernten Prinzipien lassen sich direkt auf komplexere geometrische Körper und praktische Problemstellungen übertragen.
Zusammenfassung
Der Gerade Keil steht als einer der fundamentalsten und praktischsten geometrischen Körper da. Seine rechtwinklige dreieckige Grundfläche und prismatische Form, verbunden mit elementaren mathematischen Beziehungen, machen ihn zu einem idealen Bindeglied zwischen theoretischer Geometrie und praktischer Anwendung. Von seiner Rolle im Geometrieunterricht bis zu seinen vielfältigen technischen Anwendungen zeigt er, wie mathematische Einfachheit und praktische Vielseitigkeit eine perfekte Einheit bilden können. Als Grundbaustein der räumlichen Geometrie bleibt er ein unverzichtbares Element für Ingenieure, Architekten, Lehrer und alle, die die Schönheit klarer geometrischer Formen zu schätzen wissen.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder