Quadratische Säule Rechner
Rechner und Formeln zur Berechnung einer quadratischen Säule
Quadratische Säule Rechner
Die Quadratische Säule
Eine Quadratische Säule ist ein prismatischer Körper mit quadratischer Grundfläche und vertikaler Ausdehnung.
Quadratische Säule Eigenschaften
Das Prisma: Quadratische Grundfläche mit vertikaler Ausdehnung
Quadratische Säule Struktur
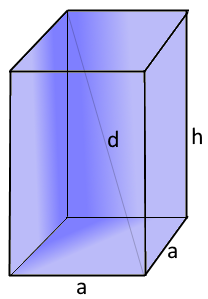
Der elegante prismatische Körper mit quadratischer Basis.
Spezialfall des Prismas mit quadratischer Grundfläche.
|
|
Was ist eine Quadratische Säule?
Eine Quadratische Säule ist ein eleganter prismatischer Körper:
- Definition: Prisma mit quadratischer Grund- und Deckfläche
- Grundfläche: Quadrat mit Seitenlänge a
- Deckfläche: Kongruentes Quadrat parallel zur Grundfläche
- Seitenflächen: Vier kongruente Rechtecke
- Höhe: Vertikaler Abstand h zwischen den Quadraten
- Spezialfall: Würfel bei a = h
Geometrische Eigenschaften der Quadratischen Säule
Die Quadratische Säule zeigt charakteristische prismatische Eigenschaften:
Grundstruktur
- 6 Flächen: 2 quadratische + 4 rechteckige Flächen
- 8 Ecken: Je 4 auf Grund- und Deckfläche
- 12 Kanten: 8 vertikale + 4 horizontale
- Rechte Winkel: Alle Innenwinkel sind 90°
Besondere Eigenschaften
- Prismatische Form: Parallele kongruente Grundflächen
- Rotationssymmetrie: 4-fache Drehsymmetrie um die Höhenachse
- Spiegelsymmetrie: 4 Symmetrieebenen
- Einfache Parameter: Nur a und h bestimmen alles
Mathematische Beziehungen
Die Quadratische Säule folgt einfachen prismatischen Gesetzen:
Volumen V
Grundfläche (a²) mal Höhe (h). Klassische Prisma-Volumenformel.
Oberfläche S
Zwei Quadrate plus vier Rechtecke. Grund- und Deckfläche plus Mantelfläche.
Anwendungen der Quadratischen Säule
Quadratische Säulen finden vielfältige praktische Anwendung:
Architektur & Bauwesen
- Säulen und Stützen in der Architektur
- Pfeiler und Träger im Brückenbau
- Schornsteine und Türme
- Fundamentpfosten und Stützpfeiler
Industrie & Technik
- Maschinenbauteile und Wellen
- Rohre und Leitungen (quadratischer Querschnitt)
- Tragstrukturen und Rahmen
- Container und Behälter
Design & Kunst
- Skulpturen und Kunstinstallationen
- Möbeldesign (Tischbeine, Stützen)
- Architektonische Gestaltungselemente
- Dekorative Säulen und Monumente
Bildung & Forschung
- Geometrie-Unterricht und Prisma-Studien
- Volumen- und Oberflächenberechnungen
- Materialwissenschaft und Festigkeitslehre
- 3D-Modellierung und CAD-Design
Formeln für die Quadratische Säule
Volumen V
Grundfläche mal Höhe
Oberfläche S
Zwei Quadrate plus vier Rechtecke
Raumdiagonale d
Diagonale durch den gesamten Körper
Grundflächendiagonale
Diagonale des quadratischen Grundrisses
Teilflächen
\[A_{Grund} = a^2\]
\[A_{Seite} = ah\]
\[A_{Mantel} = 4ah\]
Aufschlüsselung der Oberflächenbestandteile
Umfänge und Winkel
\[U = 4a\]
90°
Verhältnis h:a
Zusätzliche geometrische Eigenschaften
Berechnungsbeispiel für eine Quadratische Säule
Gegeben
Gesucht: Alle Eigenschaften der quadratischen Säule
1. Volumen berechnen
Das Volumen beträgt 200 Kubikzentimeter
2. Oberfläche berechnen
Die Oberfläche beträgt 210 Quadratzentimeter
3. Raumdiagonale
Die Raumdiagonale beträgt etwa 10,68 cm
4. Grundflächendiagonale
Die Grundflächendiagonale beträgt etwa 7,07 cm
5. Detailierte Flächenaufschlüsselung
Die elegante quadratische Säule mit ihren charakteristischen Proportionen
Die Quadratische Säule: Eleganz in der Vertikalen
Die Quadratische Säule verkörpert die perfekte Verbindung von geometrischer Klarheit und architektonischer Eleganz. Als Spezialfall des Prismas mit quadratischer Grundfläche vereint sie die Einfachheit der zweidimensionalen Quadratgeometrie mit der Ausdehnung in die dritte Dimension. Von den antiken griechischen Tempeln bis zu modernen Wolkenkratzern ist die quadratische Säule ein Symbol für Stabilität, Ordnung und zeitlose Schönheit in Architektur und Design.
Die Geometrie der Quadratischen Säule
Die Quadratische Säule fasziniert durch ihre strukturelle Klarheit:
- Quadratische Grundfläche: Alle vier Seiten haben die gleiche Länge a
- Prismatische Form: Konstanter Querschnitt über die gesamte Höhe h
- Sechs Flächen: Zwei identische Quadrate und vier identische Rechtecke
- Rechte Winkel: Alle 24 Innenwinkel sind exakt 90°
- Vertikale Ausrichtung: Die Höhe h steht senkrecht zur Grundfläche
- Symmetrieachsen: 4-fache Rotationssymmetrie um die Höhenachse
- Einfache Parameter: Nur zwei Maße (a, h) bestimmen alle Eigenschaften
Prismatische Prinzipien
Volumenberechnung
Die Formel V = a²·h zeigt das fundamentale Prisma-Prinzip: Grundfläche mal Höhe. Diese Einfachheit macht die quadratische Säule zu einem idealen Beispiel für Volumenberechnungen.
Oberflächenstruktur
S = 2a² + 4ah gliedert sich in Grundfläche (a²), Deckfläche (a²) und Mantelfläche (4ah). Diese klare Aufteilung erleichtert Materialberechnungen erheblich.
Proportionalität
Das Verhältnis h:a bestimmt den Charakter der Säule: niedrige Säulen (h < a) wirken gedrungen, hohe Säulen (h > a) erscheinen elegant und schlank.
Geometrische Harmonie
Die 4-fache Rotationssymmetrie und die rechtwinklige Struktur verleihen der quadratischen Säule eine natürliche Harmonie und visuelle Balance.
Architektonische Bedeutung
Die quadratische Säule ist ein Eckpfeiler der Architekturgeschichte:
Strukturelle Vorteile
Quadratische Säulen bieten optimale Tragfähigkeit bei minimaler Grundfläche. Die gleichmäßige Lastverteilung in alle vier Richtungen macht sie ideal für Stützfunktionen.
Designflexibilität
Die schlichte Form erlaubt vielfältige architektonische Gestaltung: von minimalistisch-modern bis klassisch-ornamental können quadratische Säulen jeden Stil unterstützen.
Rasterintegration
Quadratische Säulen fügen sich perfekt in orthogonale Raster ein, was die Planung und Konstruktion von Gebäuden erheblich vereinfacht und standardisiert.
Wirtschaftlichkeit
Die einfache Geometrie minimiert Produktionskosten und ermöglicht effiziente Fertigung, Transport und Montage von Bauelementen.
Historische Entwicklung
Die Verwendung quadratischer Säulen spiegelt die Entwicklung der Baukunst wider:
- Ägyptische Architektur: Massive Steinsäulen in Tempeln und Palästen
- Römische Baukunst: Systematische Verwendung in Aquädukten und Basiliken
- Mittelalterliche Gotik: Schlanke Pfeiler in Kathedralen
- Moderne Architektur: Stahlbeton-Säulen in Hochhäusern
- Zeitgenössisches Design: Experimentelle Formen und Materialien
- Nachhaltiges Bauen: Optimierte Ressourcennutzung
- Digitale Architektur: Parametrische Säulendesigns
Technische Anwendungen
Maschinenbau
Quadratische Wellen und Stäbe bieten präzise Führung und einfache Lagerung. Die flachen Seiten erleichtern die Kraftübertragung und Befestigung von Komponenten.
Statik und Festigkeit
Bei gleicher Querschnittfläche bietet der quadratische Querschnitt höhere Biegesteifigkeit als runde Profile, was ihn für Strukturanwendungen attraktiv macht.
Modulares Design
Quadratische Säulen ermöglichen modulare Bausysteme mit standardisierten Verbindungen, was Flexibilität und Austauschbarkeit in komplexen Strukturen gewährleistet.
Fertigungstechnik
Die prismatische Form erlaubt effiziente Herstellungsverfahren wie Extrusion, Gießen oder additive Fertigung mit minimalen Nachbearbeitungsschritten.
Mathematische Eleganz
Skalierungsgesetze
Bei proportionaler Vergrößerung (a → k·a, h → k·h) skaliert das Volumen mit k³, die Oberfläche mit k². Diese Gesetzmäßigkeiten sind fundamental für Materialberechnungen.
Optimierungspotential
Für gegebenes Volumen kann durch Variation des Verhältnisses h:a die Oberfläche minimiert werden, was in der Praxis zu Materialeinsparungen führt.
Geometrische Beziehungen
Die Raumdiagonale d = √(2a² + h²) verknüpft alle drei Raumdimensionen und zeigt die dreidimensionale Ausdehnung des ansonsten planaren Quadrats.
Symmetrieeigenschaften
Die Dihedergruppe D₄ beschreibt die Symmetrien der quadratischen Säule und ermöglicht mathematische Analysen von Spannungsverteilungen und Schwingungsmoden.
Kulturelle und symbolische Bedeutung
Symbolik der Vertikale
Säulen symbolisieren in vielen Kulturen die Verbindung zwischen Erde und Himmel, Stabilität und Streben nach oben. Die quadratische Form verstärkt das Gefühl von Ordnung und Beständigkeit.
Architektonische Sprache
Quadratische Säulen kommunizieren Klarheit, Rationalität und Moderne. Sie sind ein wesentliches Vokabular der zeitgenössischen Architektursprache.
Bildungswert
Als anschauliches Beispiel für Prisma-Geometrie vermittelt die quadratische Säule grundlegende Konzepte der Raumgeometrie und bildet eine Brücke zwischen 2D- und 3D-Denken.
Universelle Form
Die Einfachheit und Klarheit der quadratischen Säule macht sie zu einer universell verständlichen und kulturübergreifend akzeptierten geometrischen Form.
Zusammenfassung
Die Quadratische Säule steht als Sinnbild für die Kraft der geometrischen Einfachheit. Ihre perfekte Verbindung von mathematischer Klarheit und praktischer Funktionalität macht sie zu einem der vielseitigsten und wichtigsten Bauelemente in Architektur und Technik. Von den monumentalen Säulen antiker Tempel bis zu den schlanken Stützen moderner Wolkenkratzer verkörpert sie zeitlose Eleganz und strukturelle Integrität. Als Spezialfall des Prismas demonstriert sie exemplarisch, wie einfache geometrische Prinzipien zu komplexen und funktionalen Strukturen führen können. Die quadratische Säule wird auch in Zukunft eine zentrale Rolle in der Entwicklung nachhaltiger und effizienter Bauformen spielen, wo ihre mathematische Durchschaubarkeit und konstruktive Klarheit neue Innovationen ermöglichen.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder