Regelmäßiges Sechseckprisma berechnen
Rechner und Formel zur Berechnung eines regelmäßigen Sechseckprisma
Sechseckprisma Rechner
Das regelmäßige Sechseckprisma
Ein regelmäßiges Sechseckprisma hat eine sechseckige Grundfläche mit rechteckigen Seitenflächen.
Sechseckprisma Eigenschaften
Das Sechseckprisma: Prisma mit regelmäßiger sechseckiger Grund- und Deckfläche
Sechseckprisma Struktur
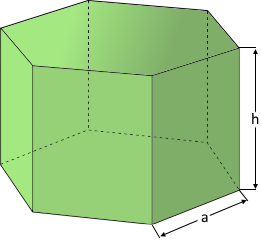
Das regelmäßige Sechseckprisma mit sechseckiger Grundfläche.
Rechteckige Seitenflächen verbinden die Sechseckflächen.
Sechseck-Eigenschaften
|
|
Was ist ein regelmäßiges Sechseckprisma?
Ein regelmäßiges Sechseckprisma ist ein geometrischer Körper mit besonderen Eigenschaften:
- Definition: Prisma mit regelmäßiger sechseckiger Grund- und Deckfläche
- Grundfläche: Regelmäßiges Sechseck mit 6 gleichen Seiten und Winkeln
- Seitenflächen: 6 kongruente Rechtecke
- Symmetrie: Rotations- und Spiegelsymmetrie
- Kanten: 18 Kanten (12 an den Sechsecken, 6 verbindend)
- Ecken: 12 Ecken (6 oben, 6 unten)
Geometrische Eigenschaften des Sechseckprismas
Das regelmäßige Sechseckprisma zeigt faszinierende geometrische Eigenschaften:
Sechseck-Eigenschaften
- Seitenlänge (a): Alle 6 Seiten sind gleich lang
- Innenwinkel: Jeder Winkel beträgt 120°
- Außenwinkel: Jeder Außenwinkel beträgt 60°
- Symmetrie: 6-fache Rotationssymmetrie
Besondere Eigenschaften
- Bienenwaben-Form: Natürliche optimale Packung
- Euler-Formel: E - K + F = 2 (12 - 18 + 8 = 2)
- Tessellation: Lückenlose Parkettierung möglich
- Stabilität: Sehr stabile geometrische Form
Mathematische Beziehungen
Das Sechseckprisma folgt eleganten mathematischen Gesetzmäßigkeiten:
Volumen Formel
Das Volumen ist das Produkt aus sechseckiger Grundfläche und Höhe. Der Faktor 1.5√3 ≈ 2.598 ist charakteristisch für das Sechseck.
Grundfläche Formel
Die Grundfläche eines regelmäßigen Sechsecks. Entspricht 6 gleichseitigen Dreiecken.
Anwendungen des Sechseckprismas
Sechseckprismen finden vielfältige Anwendungen in Natur und Technik:
Natur & Biologie
- Bienenwaben - optimale Raumnutzung
- Kristallstrukturen in der Mineralogie
- Schneeflocken und Eiskristalle
- Basaltsäulen in der Geologie
Technik & Industrie
- Sechskantschrauben und Muttern
- Wabenstrukturen in der Luft- und Raumfahrt
- Honeycomb-Materialien für Leichtbau
- Optische Fiberstrukturen
Architektur & Design
- Moderne Gebäudefassaden
- Tessellierte Bodenbeläge
- Strukturelle Wabenelemente
- Dekorative Muster und Ornamente
Bildung & Forschung
- Geometrieunterricht und Visualisierung
- Materialwissenschaftliche Forschung
- Optimierungsprobleme in der Mathematik
- Packungsprobleme und Tessellationen
Formeln für das regelmäßige Sechseckprisma
Basisfläche A
Grundfläche eines regelmäßigen Sechsecks
Oberfläche S
Zwei Sechseckflächen plus sechs Rechteckflächen
Volumen V
Grundfläche mal Höhe
Höhe h (aus Volumen)
Umstellung der Volumenformel nach h
Sechseck-Eigenschaften
α = 120°
R = a
r = a·√3/2
Wichtige Eigenschaften des regelmäßigen Sechsecks
Berechnungsbeispiel für ein Sechseckprisma
Gegeben
Gesucht: Grundfläche, Oberfläche und Volumen des Sechseckprismas
1. Grundfläche berechnen
Die Grundfläche beträgt etwa 64.95 Flächeneinheiten
2. Volumen berechnen
Das Volumen beträgt etwa 779.4 Volumeneinheiten
3. Seitenflächen berechnen
Die Seitenflächen haben zusammen 360 Flächeneinheiten
4. Oberfläche berechnen
Die Oberfläche beträgt etwa 489.9 Flächeneinheiten
5. Zusammenfassung der Ergebnisse
Das Sechseckprisma mit seiner eleganten und effizienten Geometrie
Das Sechseckprisma: Die Perfektion der sechseckigen Geometrie
Das regelmäßige Sechseckprisma ist eine der elegantesten und praktisch bedeutsamsten geometrischen Formen in der Natur und Technik. Mit seiner sechseckigen Grundfläche und den rechteckigen Seitenflächen vereint es mathematische Schönheit mit optimaler Funktionalität. Von den Bienenwaben bis zu modernen Hightech-Materialien zeigt das Sechseckprisma, wie die Natur und der Mensch die gleichen geometrischen Prinzipien zur Optimierung von Raum, Material und Stabilität nutzen.
Die Geometrie des regelmäßigen Sechsecks
Das Sechseckprisma fasziniert durch die einzigartigen Eigenschaften seiner Grundfläche:
- Sechseckige Symmetrie: Das regelmäßige Sechseck hat 6-fache Rotationssymmetrie
- Optimale Parkettierung: Sechsecke können die Ebene lückenlos und überlappungsfrei füllen
- Innenwinkel 120°: Jeder Innenwinkel beträgt exakt 120°, was 2π/3 Radiant entspricht
- Konstante Breite: Der Abstand zwischen parallelen Seiten ist konstant √3 × a
- Umkreis gleich Seitenlänge: Der Umkreisradius entspricht der Seitenlänge a
- Inkreisradius: Der Inkreisradius beträgt a × √3/2
- Teilung in Dreiecke: Kann in 6 gleichseitige Dreiecke unterteilt werden
Mathematische Eleganz und Optimierung
Isoperimetrisches Problem
Unter allen regelmäßigen Polygonen mit gleichem Umfang hat das Sechseck nach dem Kreis die zweitgrößte Fläche. Dies macht es zu einer optimalen Form für Raumaufteilungen.
Honeycombs-Vermutung
Die berühmte Honeycombs-Vermutung (bewiesen 1999) besagt, dass die sechseckige Gitterstruktur die beste Lösung für die Unterteilung der Ebene in Bereiche gleicher Fläche mit minimalem Umfang ist.
Tessellation-Eigenschaften
Regelmäßige Sechsecke sind eines der drei regelmäßigen Polygone (neben Dreiecken und Quadraten), die die Ebene periodisch tessellieren können.
Stabilitätsprinzipien
Die sechseckige Form bietet eine optimale Balance zwischen Materialverbrauch und struktureller Integrität, was ihre häufige Verwendung in technischen Anwendungen erklärt.
Die Rolle der Wurzel aus 3 in der Sechseck-Geometrie
Das Sechseckprisma ist durchdrungen von der Zahl √3:
Flächenbeziehungen
Der Faktor 1.5√3 ≈ 2.598 in der Grundflächenformel entsteht durch die Zerlegung des Sechsecks in 6 gleichseitige Dreiecke mit Fläche a²√3/4 jeweils.
Geometrische Konstruktion
√3 tritt auf als Verhältnis von Inkreis- zu Umkreisradius (√3/2), als Höhe der Teildreiecke und in allen Abstandsberechnungen innerhalb des Sechsecks.
Trigonometrische Basis
√3 = tan(60°) = cot(30°) verbindet die Sechseck-Geometrie direkt mit den Grundlagen der Trigonometrie und den Eigenschaften des gleichseitigen Dreiecks.
Physikalische Bedeutung
In kristallographischen Anwendungen bestimmt √3 die Abstände und Winkel in hexagonalen Gittern, was für viele Materialien von fundamentaler Bedeutung ist.
Natürliche und technische Anwendungen
Das Sechseckprisma findet vielfältige Anwendungen:
- Bienenwaben: Optimale Materialausnutzung bei maximaler Stabilität
- Basaltsäulen: Natürliche geologische Strukturen durch Abkühlung und Kontraktion
- Schneekristalle: Hexagonale Symmetrie durch Wassermolekül-Eigenschaften
- Carbonstrukturen: Graphit, Graphen und Kohlenstoff-Nanoröhren
- Honeycomb-Materialien: Leichtbau mit optimaler Festigkeit
- Optische Faser-Arrays: Maximale Packungsdichte
- Sechskantschrauben: Optimales Drehmoment-Übertragung
Konstruktion und Fertigungsaspekte
Präzisionsfertigung
Die Herstellung exakter Sechseckprismen erfordert präzise Winkeleinstellungen von 120° und gleichmäßige Seitenlängen. Moderne CNC-Fertigung ermöglicht Toleranzen im Mikrometerbereich.
Materialoptimierung
Die sechseckige Form ermöglicht optimale Materialausnutzung bei minimalem Verschnitt, was besonders bei teuren Materialien wirtschaftlich vorteilhaft ist.
Qualitätskontrolle
Die Überprüfung der geometrischen Korrektheit erfolgt durch Messung der Innen- und Außenwinkel, der Parallelität gegenüberliegender Seiten und der Gleichmäßigkeit aller Seitenlängen.
Toleranzmanagement
Bei Anwendungen wie Sechskantschrauben sind enge Toleranzen kritisch für die Funktionalität. DIN- und ISO-Normen definieren präzise Abmessungen und Toleranzbereiche.
Bildungsrelevanz und didaktische Aspekte
Geometrisches Verständnis
Das Sechseckprisma eignet sich hervorragend zur Demonstration von Symmetrieeigenschaften, Flächenberechnungen und räumlichen Beziehungen in der Geometrie-Ausbildung.
Interdisziplinäre Verbindungen
Es verbindet Mathematik mit Biologie (Bienenwaben), Physik (Kristallstrukturen), Chemie (Molekulargeometrie) und Technik (Materialwissenschaft).
Problemlösungskompetenzen
Die Berechnung von Sechseckprismen fördert systematisches Denken und die Anwendung mathematischer Formeln in praktischen Kontexten.
Visualisierung und Modellierung
Durch praktische Modelle und digitale Visualisierungen können abstrakte mathematische Konzepte greifbar und verständlich gemacht werden.
Zukunftsperspektiven und moderne Forschung
Nanotechnologie
In der Nanotechnologie werden hexagonale Strukturen für neuartige Materialien mit außergewöhnlichen Eigenschaften erforscht, wie Graphen und Carbon Nanotubes.
Biomimetik
Die Natur-inspirierte Forschung entwickelt neue Materialien und Strukturen basierend auf den Prinzipien der Bienenwaben und anderen hexagonalen Naturformen.
Additive Fertigung
3D-Druck-Technologien ermöglichen neue Designmöglichkeiten mit komplexen hexagonalen Innenstrukturen für optimierte Leichtbauteile.
Smart Materials
Intelligente Materialien mit hexagonalen Mikrostrukturen können ihre Eigenschaften adaptiv ändern und eröffnen neue Anwendungsfelder.
Zusammenfassung
Das regelmäßige Sechseckprisma verkörpert die perfekte Synthese aus mathematischer Eleganz und praktischer Effizienz. Seine sechseckige Grundfläche, durchdrungen von der Zahl √3 und den Prinzipien optimaler Raumaufteilung, macht es zu einer der bedeutsamsten geometrischen Formen in Natur und Technik. Von den Bienenwaben als Meisterwerk der Biooptimierung bis zu modernen Hightech-Materialien in der Luft- und Raumfahrt zeigt das Sechseckprisma, wie zeitlose mathematische Prinzipien innovative Lösungen für technische Herausforderungen bieten. Als Brücke zwischen theoretischer Geometrie und praktischer Anwendung bleibt es ein faszinierendes Studienobjekt für alle, die die Schönheit und Funktionalität der Mathematik schätzen.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder