Antiprisma Rechner
Rechner und Formeln zur Berechnung eines Antiprismas
Antiprisma Rechner
Das Antiprisma
Ein Antiprisma ist ein prismatischer Körper mit verdrehten Grundflächen (um 180°/n).
Antiprisma Eigenschaften
Das gedrehte Prisma: Grundflächen um 180°/n verdreht
Antiprisma Struktur
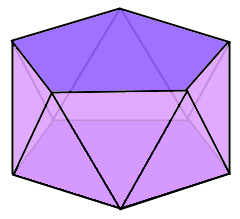
Das gedrehte Prisma mit verdrehten Grundflächen.
Verdrehung um 180°/n.
|
|
Was ist ein Antiprisma?
Ein Antiprisma ist ein faszinierender prismatischer Körper:
- Definition: Prisma mit verdrehten Grundflächen
- Verdrehung: Obere Grundfläche um 180°/n gedreht
- Seitenflächen: 2n kongruente Dreiecke
- Ecken: 2n Ecken insgesamt
- Kanten: 4n Kanten (n+n+2n)
- Regelmäßig: Alle Kanten gleich lang
Geometrische Eigenschaften des Antiprismas
Das Antiprisma zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Grundflächen: 2 regelmäßige n-Ecke
- Seitenflächen: 2n kongruente Dreiecke
- Euler-Charakteristik: V - E + F = 2n - 4n + (2n+2) = 2
- Verdrehungswinkel: 180°/n
Besondere Eigenschaften
- Chirales Objekt: Existiert in Links- und Rechtsform
- Uniforme Kanten: Alle Kanten gleich lang
- Drehsymmetrie: n-zählige Drehachse
- Semiregulär: Zwei Arten von Flächen
Mathematische Beziehungen
Das Antiprisma folgt komplexen trigonometrischen Gesetzen:
Volumen-Formel
Abhängig von cos, sin und n. Komplex aber elegant.
Oberflächen-Formel
Summe von Grundflächen und Dreiecken. Elegante trigonometrische Form.
Anwendungen des Antiprismas
Antiprismen finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Gedrehte Turmstrukturen
- Moderne Gebäudedesigns
- Strukturelle Verstrebungen
- Architektonische Elemente
Wissenschaft & Technik
- Kristallographische Strukturen
- Molekulare Geometrie
- Optische Komponenten
- Mechanische Konstruktionen
Bildung & Lehre
- Geometrie-Unterricht
- Trigonometrie-Anwendungen
- 3D-Geometrie-Studien
- Mathematische Demonstrationen
Kunst & Design
- Skulpturale Werke
- Kunstinstallationen
- Dekorative Objekte
- Geometrische Muster
Formeln zum Antiprisma
Oberfläche (S)
Oberfläche mit Cotangens und √3
Volumen (V)
Komplexe trigonometrische Volumenformel
Höhe (h)
Höhe abhängig von der Eckenzahl n
Hinweis
Winkelfunktionen benötigen Bogenmaß
Antiprisma Parameter
2 regelmäßige n-Ecke
2n Dreiecke
180°/n
Alle gleich lang
Alle Eigenschaften hängen von der Eckenzahl n der Grundfläche ab
Berechnungsbeispiel für ein Antiprisma
Gegeben
Gesucht: Alle Eigenschaften des fünfeckigen Antiprismas
1. Oberflächen-Berechnung
Für n=5:
\[S = \frac{5}{2} \cdot (\cot(36°) + \sqrt{3}) \cdot 100\] \[S ≈ 2.5 \cdot (1.376 + 1.732) \cdot 100\] \[S ≈ 777\]Die Oberfläche beträgt etwa 777 Flächeneinheiten
2. Höhen-Berechnung
Für n=5:
\[h = \sqrt{1 - \frac{1}{4 \cdot \cos^2(18°)}} \cdot 10\] \[h ≈ \sqrt{1 - 0.277} \cdot 10\] \[h ≈ 8.5\]Die Höhe beträgt etwa 8.5 Längeneinheiten
3. Das fünfeckige Antiprisma
Das fünfeckige Antiprisma mit perfekter Verdrehungssymmetrie
Das Antiprisma: Das gedrehte Prisma
Das Antiprisma ist ein faszinierender geometrischer Körper, der die Eleganz der Verdrehung verkörpert. Durch die charakteristische Rotation der oberen Grundfläche um 180°/n entsteht eine einzigartige Struktur mit 2n dreieckigen Seitenflächen, die das Antiprisma zu einem der interessantesten semiregulären Polyeder macht. Die mathematische Schönheit liegt in den komplexen trigonometrischen Beziehungen, die alle geometrischen Eigenschaften miteinander verknüpfen.
Die Geometrie der Verdrehung
Das Antiprisma zeigt die Perfektion der geometrischen Verdrehung:
- Verdrehungswinkel: Präzise 180°/n für n-eckige Grundfläche
- Chiralität: Existiert in Links- und Rechtsform
- Uniformität: Alle Kanten haben dieselbe Länge
- Semiregularität: Zwei verschiedene Flächentypen
- Symmetrie: n-zählige Drehachse
- Trigonometrie: Komplexe Sinus- und Cosinus-Beziehungen
- Vielseitigkeit: Funktioniert für jede Eckenzahl n ≥ 3
Mathematische Eleganz
Trigonometrische Perfektion
Die Formeln des Antiprismas sind Meisterwerke der Trigonometrie, die zeigen, wie Sinus, Cosinus und Cotangens zusammenwirken, um die verdrehte Geometrie zu beschreiben.
Parametrische Vielfalt
Durch Variation der Eckenzahl n entstehen unendlich viele verschiedene Antiprismen, vom dreieckigen bis zu hocheckigen Formen mit unterschiedlichen ästhetischen Qualitäten.
Strukturelle Innovation
Die Verdrehung erzeugt eine optimale Verteilung der Spannungen und macht Antiprismen zu bevorzugten Strukturen in Architektur und Ingenieurtechnik.
Ästhetische Vollendung
Die harmonische Kombination aus regelmäßigen Grundflächen und gleichmäßig verdrehten Dreiecken erzeugt eine einzigartige visuelle Dynamik.
Zusammenfassung
Das Antiprisma verkörpert die perfekte Balance zwischen mathematischer Komplexität und geometrischer Schönheit. Seine verdrehte Struktur, beschrieben durch elegante trigonometrische Formeln, macht es zu einem faszinierenden Studienobjekt für Mathematiker, Architekten und Designer. Von der einfachen dreieckigen Form bis zu komplexen vieleckigen Varianten zeigt das Antiprisma, wie die Verdrehung von Grundformen zu völlig neuen geometrischen Welten führen kann. Als Brücke zwischen theoretischer Mathematik und praktischer Anwendung bleibt das Antiprisma ein faszinierendes Beispiel für die Kraft der geometrischen Transformation.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder