Hexagonal Prism Calculator
Online calculator and formulas for calculating a hexagonal prism
Hexagonal Prism Calculator
The Hexagonal Prism
A hexagonal prism is a prismatic solid with hexagonal bases and rectangular sides. Perfect six-fold symmetry.
Hexagonal Prism Properties
The six-sided prism: Two parallel hexagonal bases connected by rectangular faces
Hexagonal Prism Structure
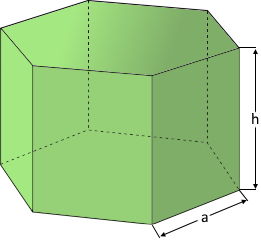
The prism with hexagonal cross-section.
Perfect six-fold rotational symmetry.
|
|
What is a Hexagonal Prism?
A hexagonal prism is a fundamental prismatic shape with remarkable properties:
- Definition: Prism with hexagonal cross-section
- Bases: Two parallel regular hexagons
- Sides: Six rectangular faces
- Vertices: 12 vertices total
- Edges: 18 edges (6+6+6)
- Symmetry: Six-fold rotational symmetry
Geometric Properties of the Hexagonal Prism
The hexagonal prism displays beautiful geometric characteristics:
Hexagonal Parameters
- Bases: 2 regular hexagons
- Side faces: 6 rectangles
- Internal angles: 120° in hexagon
- Euler formula: V - E + F = 12 - 18 + 8 = 2
Special Properties
- Tessellation: Hexagons tile the plane perfectly
- Natural occurrence: Found in honeycombs
- Efficiency: Maximum area for given perimeter
- Six-fold symmetry: Rotational and reflection symmetry
Mathematical Relationships
The hexagonal prism follows elegant mathematical principles:
Square Root Relationships
Hexagonal areas involve √3. Elegant and precise formulas.
Practical Calculations
Clear relationships between dimensions. Easy to compute and understand.
Applications of the Hexagonal Prism
Hexagonal prisms are found everywhere in nature and technology:
Nature & Biology
- Honeycomb structures
- Crystal formations
- Basalt columns
- Snowflake patterns
Engineering & Manufacturing
- Hex bolts and nuts
- Structural beams
- Pencil cross-sections
- Efficient packing
Architecture & Construction
- Hexagonal tiles
- Dome structures
- Modular construction
- Space frames
Games & Design
- Board game tiles
- Game grids
- Decorative patterns
- Artistic designs
Formulas for the regular hexagonal prism
Base area (A)
Area of the regular hexagonal base
Surface area (S)
Total surface area: 2 hexagons + 6 rectangles
Volume (V)
Volume equals base area times height
Height (h)
Height when volume and side length are known
Hexagon properties
120°
6a
2a
a√3/2
Key properties of the regular hexagon base
Example calculation for a Hexagonal Prism
Given
Calculate: Height and surface area of the hexagonal prism
1. Base area calculation
The base area is 64.95 square units
2. Height calculation
The height is 2.16 units
3. Surface area calculation
The surface area is 194.7 square units
4. Verification
✓ Close to given volume of 140
Calculation verified successfully
Summary
Complete analysis of the hexagonal prism with given parameters
The Hexagonal Prism: Nature's Perfect Shape
The hexagonal prism represents one of nature's most efficient and beautiful geometric forms. From the hexagonal cells in honeycomb structures to the basalt columns of Giant's Causeway, this shape demonstrates the perfect balance between structural strength and material efficiency. Its six-fold symmetry creates patterns that tile perfectly, making it an ideal choice for both natural formations and human engineering applications.
The Geometry of Efficiency
The hexagonal prism showcases mathematical and practical perfection:
- Perfect tessellation: Hexagons tile the plane without gaps or overlaps
- Maximum efficiency: Largest area for given perimeter among regular polygons
- Six-fold symmetry: Rotational symmetry every 60 degrees
- Natural occurrence: Found throughout the natural world
- Structural strength: Distributes stress efficiently
- Simple mathematics: Elegant formulas involving √3
- Practical applications: Used extensively in engineering and design
Mathematical Beauty and Natural Wisdom
Honeycomb Efficiency
Bees have discovered that hexagonal cells require the least amount of wax for maximum storage space, demonstrating nature's optimization of the hexagonal form.
Crystal Structures
Many crystals naturally form hexagonal prisms due to their atomic structure, showing how geometry emerges from molecular arrangements.
Engineering Applications
From hex bolts that resist turning to structural beams that provide strength, engineers have adopted the hexagon for its superior mechanical properties.
Mathematical Elegance
The hexagonal prism's formulas involve √3, connecting it to the fundamental relationships in geometry and trigonometry.
Conclusion
The hexagonal prism stands as a testament to the unity of mathematical beauty and practical efficiency. Its appearance throughout nature - from snowflakes to basalt formations - demonstrates that certain geometric forms represent optimal solutions to physical constraints. In human applications, from ancient architecture to modern manufacturing, the hexagonal prism continues to prove its worth as both a structural element and an aesthetic choice. For students of geometry, it provides an excellent example of how mathematical principles manifest in the real world, bridging the gap between abstract theory and tangible applications. The hexagonal prism truly embodies the perfect marriage of form and function, efficiency and elegance.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron