Bessel-Je Funktion berechnen
Online Rechner zur logarithmisch skalierten Bessel-Funktion Jeᵥ(z) der ersten Art - Numerisch stabile oszillierende Zylinderfunktion
Bessel-Je Funktion Rechner
Exponentiell skalierte Bessel-Funktion
Die Jeᵥ(z) oder exponentiell skalierte Bessel-Funktion zeigt stabiles oszillierendes Verhalten als Zylinderfunktion.
Bessel-Je Funktionskurve
Mauszeiger auf der Grafik zeigt die Werte an.
Die exponentiell skalierte Form eliminiert Amplitudenwachstum bei großen z.
|
|
Warum oszillierendes Verhalten statt exponentielles Wachstum?
Die standard Bessel-Funktion unterscheidet sich fundamental von modifizierten Bessel-Funktionen:
- Periodische Oszillation: Jᵥ(z) oszilliert für große z
- Dämpfende Amplitude: Amplitude ~ 1/√z
- Physikalische Wellen: Beschreibt Schwingungs- und Wellenprozesse
- Zylindersymmetrie: Lösungen in zylindrischen Koordinaten
- Nullstellen: Unendlich viele Nullstellen bei großen z
- Asymptotik: Jᵥ(z) ~ √(2/πz) cos(z - πν/2 - π/4)
Anwendungen in Wellenproblemen und Zylindersymmetrie
Die Bessel-Je Funktion ist die numerisch stabile Lösung für oszillierende Wellenprozesse:
Mechanische Schwingungen
- Kreisförmige Membranschwingungen
- Zylinder- und Rohrschwingungen
- Akustische Resonatoren
Elektromagnetische Wellen
- Zylindrische Wellenleiter
- Antennenabstrahlung
- Hohlraumresonatoren
Formeln zur Bessel-Je Funktion
Definition
Exponentiell skalierte Bessel-Funktion
Beziehung zu Jᵥ
Umkehrung der Skalierung
Reihenentwicklung
Skalierte Potenzreihe
Asymptotische Form
Für große z (mit stabiler Amplitude)
Rekursionsformel
Gleiche Rekursion wie unscaled Version
Integraldarstellung
Für ganzzahlige Ordnung n
Spezielle Werte
Wichtige Werte
Symmetrieeigenschaften
Für ganzzahlige n
Verhalten bei z = 0
Gleiches Verhalten wie Jᵥ(0)
Anwendungsgebiete
Wellenpropagation, Schwingungsprobleme, zylindrische Geometrie, Antenna-Design.
Bessel-Je Oszillationsmuster
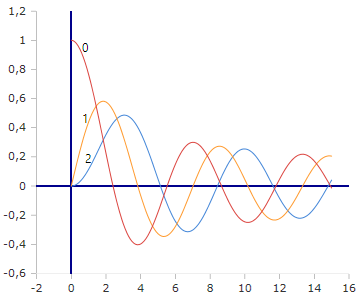
Bessel-Je Funktionen (Ordnung 0,1,2)
Die exponentiell skalierten Funktionen zeigen klare Oszillationen mit kontrollierter Amplitude ohne numerische Instabilitäten.
Charakteristische Eigenschaften
- Je₀(z) startet bei 1, oszilliert dann
- Jeₙ(z) mit n > 0 startet bei 0
- Asymptotisch: ~ √(2/πz) cos(...)
- Stabile Amplitude durch Skalierung
Ausführliche Beschreibung der Bessel-Je Funktion
Mathematische Definition
Die exponentiell skalierte Bessel-Funktion Jeᵥ(z) ist eine numerisch stabilisierte Version der standard Bessel-Funktion Jᵥ(z). Im Gegensatz zu modifizierten Bessel-Funktionen behält sie das oszillierende Verhalten bei, eliminiert aber numerische Instabilitäten.
Verwendung des Rechners
Geben Sie die Ordnungszahl ν (ganze Zahl) und das Argument z (positive reelle Zahl) ein. Der Grafik-Stretch Parameter steuert die X-Achsen-Skalierung für bessere Visualisierung.
Physikalischer Hintergrund
Die Bessel-Funktionen wurden ursprünglich von Friedrich Bessel für astronomische Berechnungen entwickelt. Sie beschreiben Wellenpropagation in zylindrischen Systemen und sind fundamental für viele physikalische Phänomene.
Eigenschaften und Anwendungen
Physikalische Anwendungen
- Kreisförmige Membranschwingungen (Trommelfell)
- Elektromagnetische Wellen in Zylinderleitern
- Akustische Resonatoren und Hohlräume
- Beugung an zylindrischen Objekten
Mathematische Eigenschaften
- Oszillierendes Verhalten für große z
- Dämpfende Amplitude ~ 1/√z
- Symmetrie: Je₋ₙ(z) = (-1)ⁿ Jeₙ(z) für ganzzahlige n
- Unendlich viele Nullstellen für z > 0
Numerische Aspekte
- Stabilität: Numerisch stabil für komplexe Argumente
- Skalierung: Eliminiert exponentielles Wachstum bei Im(z) ≠ 0
- Genauigkeit: Erhaltene Präzision in allen z-Bereichen
- Effizienz: Optimierte Algorithmen verfügbar
Interessante Fakten
- Bessel-Funktionen beschreiben die Schwingungsmoden von Trommeln
- Die Nullstellen von J₀(z) bestimmen Resonanzfrequenzen zylindrischer Hohlräume
- Bessel-Funktionen sind essentiell für die Fourier-Bessel-Transformation
- Sie treten in der Quantenmechanik bei radialsymmetrischen Problemen auf
Berechnungsbeispiele und Oszillationseigenschaften
Kleines Argument
z = π/2:
J₀(π/2) ≈ 0.567
Je₀(π/2) ≈ 0.567
Erste Nullstelle
z ≈ 2.405:
J₀(2.405) ≈ 0
Je₀(2.405) ≈ 0
Großes Argument
z = 20:
J₀(20) ≈ 0.167
Je₀(20) ≈ 0.167
Wellenanwendungen und Zylindersymmetrie
Akustische Anwendungen
Trommelfell-Schwingungen:
Radiale Moden: u(r,φ,t) = J₀(k·r) cos(ωt)
Nullstellen bestimmen Resonanzfrequenzen
Beispiel: Kreisförmige Membran mit Radius R hat Resonanzen bei k·R = Nullstellen von J₀.
Elektromagnetische Wellen
Zylindrische Wellenleiter:
TM-Moden: E_z ∝ J_m(k_c·r) e^(imφ)
Cutoff-Frequenzen durch Bessel-Nullstellen
Beispiel: TE₀₁-Mode in Hohlleiter hat niedrigste Cutoff-Frequenz.
Nullstellen und Oszillationsverhalten
Wichtige Nullstellen
J₀(z) Nullstellen:
2.405, 5.520, 8.654, 11.792, ...
J₁(z) Nullstellen:
3.832, 7.016, 10.173, 13.324, ...
Asymptotik: Nullstellen folgen αₙ ≈ (n - 1/2)π für große n.
Oszillationseigenschaften
Asymptotisches Verhalten:
Jᵥ(z) ~ √(2/πz) cos(z - νπ/2 - π/4)
Periode ≈ 2π, Amplitude ~ 1/√z
Eigenschaften: Oszillationsfrequenz bleibt konstant, nur Amplitude nimmt ab.
Numerische Berechnung und Algorithmen
Berechnungsmethoden
- Series Expansion: Für kleine |z| und kleine ν
- Asymptotic Expansion: Für große |z|
- Recurrence Relations: Für benachbarte Ordnungen
- Continued Fractions: Für spezielle Bereiche
Software-Implementierungen
- GNU GSL: Highly accurate implementations
- Boost Math: C++ template library
- SciPy: Python scipy.special.jn
- MATLAB: Built-in besselj function
|
|
|
|