Fibonacci Zahlen berechnen
Online Rechner und Formeln zur Berechnung einer Fibonacci Zahl zu einem Index
Fibonacci Zahlen Rechner
Fibonacci Zahlenfolge
Der Rechner berechnet die n-te Fibonacci Zahl aus der berühmten Zahlenfolge, bei der jede Zahl die Summe der beiden vorangehenden ist.
Fibonacci Zahlenfolge
Erste 15 Fibonacci Zahlen:
Goldener Schnitt
Das Verhältnis aufeinanderfolgender Fibonacci-Zahlen nähert sich dem Goldenen Schnitt φ ≈ 1,618 an.
Die Fibonacci-Folge erscheint häufig in der Natur: Blütenblätter, Tannenzapfen, Schneckenhäuser und Galaxienspiralen.
|
|
Formeln zur Fibonacci Zahlenfolge
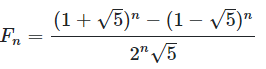
Binet'sche Formel
Wobei φ = (1+√5)/2 und ψ = (1-√5)/2
Rekursive Definition
Mit F₀ = 0 und F₁ = 1
Beispiele
Berechnungsbeispiele
- F(0) = 0
- F(1) = 1
- F(6) = 8
- F(10) = 55
- F(20) = 6765
Anwendung
Fibonacci-Zahlen werden in der Informatik, Börsenanalyse, Architektur und Kunst verwendet.
Ausführliche Beschreibung der Fibonacci-Zahlen
Mathematische Definition
Die Fibonacci-Folge ist eine unendliche Zahlenfolge, die mit 0 und 1 beginnt. Jede weitere Zahl ist die Summe der beiden vorangehenden Zahlen. Diese Folge wurde im Jahr 1202 von Leonardo Fibonacci in seinem Werk "Liber Abaci" beschrieben.
Verwendung des Rechners
Geben Sie den Index (beginnend mit 0) ein und klicken Sie auf 'Rechnen'. Der Rechner verwendet die Binet'sche Formel für eine effiziente Berechnung.
Eigenschaften
- Wachstum: Exponentielles Wachstum mit Basis φ
- Verhältnisse: Fₙ₊₁/Fₙ → φ (Goldener Schnitt)
- Identitäten: Cassini-Identität, Katalan-Identität
Anwendungen und Vorkommen
In der Natur
- Blütenblätter (Lilien: 3, Butterblumen: 5)
- Tannenzapfen und Ananas (Spiralen)
- Sonnenblumenkerne (Spiralmuster)
- Nautilus-Schneckenhäuser
In der Technik
- Algorithmen und Datenstrukturen
- Fibonacci-Heap in der Informatik
- Optimierung und Suchalgorithmen
- Pseudo-Zufallszahlengenerierung
In Kunst und Architektur
- Goldener Schnitt in Gemälden
- Architektonische Proportionen
- Musikkomposition und Harmonielehre
- Fotografie (Drittel-Regel)
Interessante Fakten
- Jede 3. Fibonacci-Zahl ist gerade
- Summe der ersten n Fibonacci-Zahlen: Fₙ₊₂ - 1
- Das Kaninchenproblem führte zur Entdeckung
- Verwandt mit dem Goldenen Schnitt
|
|
|
|