Bessel-K Funktion berechnen
Online Rechner zur modifizierten Bessel-Funktion Kᵥ(z) der zweiten Art - Exponentiell abfallende Lösungen für physikalische Systeme
Bessel-K Funktion Rechner
Modifizierte Bessel-Funktion zweiter Art
Die Kᵥ(z) oder modifizierte Bessel-Funktion zweiter Art zeigt exponentiell abfallendes Verhalten und beschreibt gedämpfte Prozesse.
Bessel-K Funktionskurve
Mauszeiger auf der Grafik zeigt die Werte an.
Die K-Funktion zeigt exponentiell abfallendes Verhalten für große z.
|
|
Warum exponentiell abfallendes Verhalten?
Die modifizierte Bessel-Funktion zweiter Art unterscheidet sich fundamental von der ersten Art:
- Exponentieller Abfall: Kᵥ(z) → 0 für z → ∞
- Singularität bei z=0: Kᵥ(0) → ∞
- Physikalische Dämpfung: Beschreibt Diffusion und Wärmeverlust
- Komplementäre Funktion: Partner zu Iᵥ(z)
- Randwertprobleme: Wichtig für unendliche Gebiete
- Asymptotik: Kᵥ(z) ~ √(π/2z) e^(-z)
Physikalische Anwendungen der Bessel-K Funktion
Die Bessel-K Funktion ist unverzichtbar für Dämpfungs- und Diffusionsprozesse:
Wärmeleitung
- Wärmeabfuhr in unendlichen Gebieten
- Stationäre Temperaturverteilungen
- Kühlkörper und Wärmetauscher
Diffusionsprozesse
- Konzentrationsgradiente
- Massentransport in Materialien
- Poröse Medien und Filtration
Formeln zur Bessel-K Funktion
Definition
Definition über modifizierte Bessel-Funktionen erster Art
Für ganzzahlige ν
Grenzwertdefinition für ganzzahlige Ordnungen
Integraldarstellung
Integralform für Re(z) > 0
Asymptotische Form
Für große z (exponentieller Abfall)
Rekursionsformel
Rekursion für benachbarte Ordnungen
Symmetrieeigenschaft
Symmetrie bzgl. der Ordnung
Verhalten bei z → 0
Singularität im Ursprung
Spezielle Werte
Wichtige Werte
Symmetrieeigenschaften
Für alle reellen ν
Singularität bei z = 0
Für alle ν ≥ 0
Verhalten bei z → ∞
Exponentieller Abfall
Anwendungsgebiete
Wärmeleitung, Diffusion, elektromagnetische Abschirmung, Quantenfeldtheorie.
Bessel-K Abfallverhalten
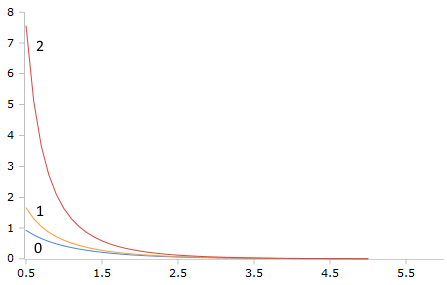
Bessel-K Funktionen (Ordnung 0,1,2)
Die K-Funktionen zeigen charakteristischen exponentiellen Abfall mit Singularitäten bei z = 0 und verschiedenen Abfallraten je nach Ordnung.
Charakteristische Eigenschaften
- Kᵥ(z) → ∞ für z → 0⁺
- Kᵥ(z) → 0 für z → ∞
- Asymptotisch: ~ √(π/2z) e^(-z)
- Monoton abfallend für alle z > 0
Ausführliche Beschreibung der Bessel-K Funktion
Mathematische Definition
Die modifizierte Bessel-Funktion zweiter Art Kᵥ(z) ist die zweite linear unabhängige Lösung der modifizierten Bessel-Differentialgleichung. Im Gegensatz zu Iᵥ(z) zeigt sie exponentiell abfallendes Verhalten und ist bei z = 0 singulär.
Verwendung des Rechners
Geben Sie die Ordnungszahl ν (ganze Zahl) und das Argument z (positive reelle Zahl) ein. Die K-Funktion ist nur für z > 0 definiert aufgrund der Singularität bei z = 0.
Physikalischer Hintergrund
Die Bessel-K Funktionen beschreiben Dämpfungs- und Abfallprozesse in zylindrischen Geometrien. Sie sind besonders wichtig für Probleme mit unendlichen Randbedingungen, wo physikalische Größen im Unendlichen verschwinden müssen.
Eigenschaften und Anwendungen
Physikalische Anwendungen
- Wärmeleitung in unendlichen zylindrischen Medien
- Diffusionsprozesse mit Randbedingungen im Unendlichen
- Elektromagnetische Abschirmung und Skin-Effekt
- Quantenfeldtheorie und Teilchenphysik
Mathematische Eigenschaften
- Exponentieller Abfall für große z
- Singularität bei z = 0
- Symmetrie: K₋ᵥ(z) = Kᵥ(z)
- Monoton abfallend für alle z > 0
Numerische Aspekte
- Stabilität: Numerisch herausfordernd für kleine z
- Algorithmen: Spezielle Methoden für verschiedene z-Bereiche
- Genauigkeit: Hohe Präzision bei großen z
- Effizienz: Rekursionsformeln für benachbarte Ordnungen
Interessante Fakten
- K₀(z) ist wichtig für logarithmische Potentiale in 2D
- K₁(z) tritt in der Relativitätstheorie bei thermischen Gleichgewichten auf
- K-Funktionen sind essentiell für Greensche Funktionen in der Physik
- Sie beschreiben das Verhalten von Feldern bei großen Entfernungen
Berechnungsbeispiele und Abfallverhalten
Kleines Argument
z = 0.5:
K₀(0.5) ≈ 0.924
K₁(0.5) ≈ 1.656
Mittleres Argument
z = 2:
K₀(2) ≈ 0.114
K₁(2) ≈ 0.140
Großes Argument
z = 10:
K₀(10) ≈ 1.78×10⁻⁵
Starker exponentieller Abfall
Detaillierte physikalische Anwendungen
Wärmeleitung
Stationäre Wärmeleitung:
T(r) = A K₀(r/λ) für zylindrische Wärmequelle
λ ist die charakteristische Länge
Beispiel: Kühlkörper mit exponentiell abfallender Temperatur.
Elektromagnetismus
Skin-Effekt:
E(r) ∝ K₀(r/δ) in leitfähigem Medium
δ ist die Skin-Tiefe
Beispiel: Elektromagnetische Abschirmung und Eindringtiefe.
Mathematische Eigenschaften und Relationen
Asymptotisches Verhalten
Für große z:
Kᵥ(z) ~ √(π/2z) e^(-z)
Für kleine z (ν > 0):
Kᵥ(z) ~ Γ(ν)/2 (2/z)^ν
Besonderheit: K₀(z) ~ -ln(z) für kleine z.
Beziehungen zu anderen Funktionen
Wronskische Determinante:
W[Iᵥ, Kᵥ] = -1/z
Beziehung zu Hankel-Funktionen:
Kᵥ(z) = (π/2)i^(ν+1) H^(1)_ν(iz)
Bedeutung: Fundamentales Lösungssystem mit Iᵥ(z).
Spezielle Ordnungen und Grenzfälle
Ordnung ν = 0
K₀(z) - Fundamentallösung:
Logarithmische Singularität bei z = 0
Anwendung: 2D-Probleme, logarithmische Potentiale.
Ordnung ν = 1
K₁(z) - Ableitung von K₀:
Wichtig für Gradientenprobleme
Anwendung: Diffusionsflüsse, thermische Gradienten.
Numerische Berechnung und Algorithmen
Berechnungsmethoden
- Series Expansion: Für kleine z (mit Vorsicht bei Singularität)
- Asymptotic Expansion: Für große z ≥ 15
- Recurrence Relations: Für benachbarte Ordnungen
- Continued Fractions: Für mittlere z-Bereiche
Software-Implementierungen
- GNU GSL: Hochpräzise K-Funktionen
- Boost Math: C++ Template-Bibliothek
- SciPy: Python scipy.special.kv
- MATLAB: Built-in besselk Funktion
|
|
|
|