Bessel-Y Funktion berechnen
Online Rechner zur Berechnung der Bessel-Funktion Yv(z) der zweiten Art
Der Rechner auf dieser Seite berechnet die Bessel-Funktion Yv(z) für reelle Zahlen. Bessel Funktionen für komplexe Zahlen finden Sie im Bereich der komplexen Zahlen.
Zur Berechnung geben die Ordnungszahl und das Argument z ein. Dann klicken Sie den Button 'Rechnen'. Die Ordnungszahl muss eine ganze Zahl sein und das Argument z muss positiv sein.
Durch Ändern des Werts „Grafik strecken“ kann die Skala der X-Achse verlängert oder verkürzt werden.
|
Bessel-Y Funktion der zweiten Art
Die Funktion Bessel-Y berechnet die Bessel Funktion Yv(z) der zweiten Art. Die Bessel-Y Funktionen weisen ein oszillierendes (kein exponentielles) Verhalten auf. Bessel-Y (n, z) ist eine Lösung der Bessel-Differentialgleichung.
Das Resultatist eine komplexe Zahl, wenn z negativ und n eine Dezimalzahl ist.
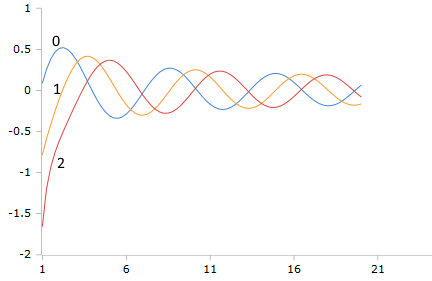
Plot der Bessely Funktion mit den Ordnungszahlen 0, 1 und 2
Definition der Bessel Funktionen
Bessel-Funktionen erster Gattung (Jν)
Die Bessel-Funktion erster Gattung n-ter Ordnung ist definiert als:
\(\displaystyle J_{\nu}(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu} \)
Hierbei ist \( \Gamma \) die Gammafunktion.
Im Ursprung (\( z = 0 \)) sind diese Funktionen für ganzzahlige Werte von \( \nu \) endlich.
Für nicht-ganzzahlige Werte von \( \nu \) gibt es zwei linear unabhängige Lösungen.
Für ganzzahlige Werte von \( \nu \) gilt die Beziehung:
\(\displaystyle J_{-\nu}(z) = (-1)^{\nu} J_{\nu}(z) \)
Bessel-Funktionen zweiter Gattung (Yν)
Die Bessel-Funktion zweiter Gattung n-ter Ordnung ist definiert als:
\(\displaystyle Y_{\nu}(z) = \frac{J_{\nu}(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)} \)
Modifizierte Bessel-Funktionen (Iν, Kν)
Die modifizierte Bessel-Funktion erster Art n-ter Ordnung ist definiert als:
\(\displaystyle I_{\nu}(z) = i^{-\nu} J_{\nu}(iz) \)
Die modifizierte Bessel-Funktion zweiter Art n-ter Ordnung ist definiert als:
\(\displaystyle K_{\nu}(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_{\nu}(z)}{\sin(\nu \pi)} \)
Weitere Spezial Funktionen
Airy • Abgeleitete Airy • Bessel I • Bessel Ie • Bessel J • Bessel Je • Bessel K • Bessel Ke • Bessel Y • Bessel Ye • Bessel Jv • Bessel Yv • Hankel • Beta • Unvollständige Beta • Inverse Unvollständige Beta • Binomialkoeffizient • Logarithmus des Binomialkoeffizienten • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma Funktion • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Modifizierte Struve • Struve Tabelle • Modifizierte Struve Tabelle • Riemann ZetaInformationen zu Bessel Funktionen
Die Bessel-Funktionen sind eine Gruppe spezieller mathematischer Funktionen, die in verschiedenen physikalischen und mathematischen Anwendungen auftreten. Sie wurden ursprünglich von dem Mathematiker Daniel Bernoulli definiert und später von Friedrich Bessel verallgemeinert. Diese Funktionen sind Lösungen der Bessel-Gleichung für einen beliebigen komplexen Parameter \( \alpha \), der die Ordnung der Bessel-Funktion repräsentiert.
Es gibt zwei Hauptklassen von Bessel-Funktionen:
-
Bessel-Funktion erster Art (Jα): Diese Funktionen sind Lösungen der Bessel-Differentialgleichung,
die am Ursprung nicht singulär sind.
Sie werden manchmal auch als Zylinderfunktionen oder Zylinderschwingungen bezeichnet.
- Bessel-Funktion zweiter Art (Yα): Im Gegensatz zu den gewöhnlichen Bessel-Funktionen, die als Funktionen eines reellen Arguments oszillieren, wachsen die Funktionen \(I_\alpha\) exponentiell, während die Funktionen \(K_\alpha\) exponentiell abklingen. Wie die gewöhnliche Bessel-Funktion \(J_\alpha\) geht die Funktion \(I_\alpha\) für \(x = 0\) gegen null, wenn \( \alpha > 0 \), und ist für \(x = 0\) endlich, wenn \( \alpha = 0 \).
Diese Funktionen spielen eine wichtige Rolle bei der Beschreibung von Schwingungen einer kreisförmigen Membran, elektromagnetischen Wellen in zylindrischen Wellenleitern, Wärmeleitung in zylindrischen Objekten, akustischen Membranen (wie Trommelfellen) und vielem mehr. Sie sind ein unverzichtbares Werkzeug für viele Probleme der Wellenausbreitung und statischer Potentiale in der Physik und Ingenieurwissenschaften.
|
|