Derivative Softsign Funktion berechnen
Online Rechner zur Berechnung der Ableitung der Softsign Funktion - Sanfte Gradientenfunktion für neuronale Netze
Softsign Ableitung Rechner
Softsign Ableitung
Die softsign'(x) oder Softsign-Ableitung ist eine sanfte Gradientenfunktion für stabiles Training neuronaler Netze.
Sanfte Glockenförmige Kurve
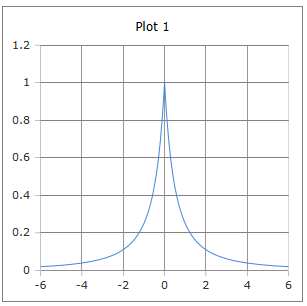
Kurve der derivativen Softsign Funktion: Sanfte Glockenkurve mit Maximum bei x = 0.
Eigenschaften: Maximum 0.25 bei x = 0, immer positiv, langsamer abfallend als Sigmoid.
|
|
Warum ist die Softsign-Ableitung sanfter?
Die sanfte Glockenform der Softsign-Ableitung bietet Vorteile für das Training neuronaler Netze:
- Langsamer Abfall: Weniger abrupte Gradientenänderungen
- Immer positiv: Keine negativen Gradienten
- Symmetrie: Gleichmäßige Form links und rechts
- Sanfte Sättigung: Weniger vanishing gradients
- Computational effizient: Einfache Berechnung
- Stabilität: Bessere numerische Eigenschaften
Sanfte Gradienten für stabiles Training
Die einfache Form softsign'(x) = 1/(1+|x|)² macht die Berechnung effizient und stabil:
Die sanfte Ableitung führt zu gleichmäßigeren Gradientenflüssen und stabilerer Konvergenz im Vergleich zu anderen Aktivierungsfunktionen.
Formeln zur Softsign Ableitung
Grundformel
Einfache rationale Funktion
Symmetrie
Gerade Funktion
Stückweise Form
Aufgeteilte Darstellung
Kettenregel Form
Für zusammengesetzte Funktionen
Maximumseigenschaft
Maximum bei x = 0
Eigenschaften
Spezielle Werte
Definitionsbereich
Alle reellen Zahlen
Wertebereich
Zwischen 0 und 1
Anwendung
Backpropagation, sanfte Gradienten, stabiles Training, alternative zu Sigmoid-Ableitung.
Asymptotisches Verhalten
Geht gegen 0 für große |x|
Ausführliche Beschreibung der Softsign Ableitung
Mathematische Definition
Die Ableitung der Softsign-Funktion ist eine sanfte, glockenförmige Funktion, die eine wichtige Rolle beim Training neuronaler Netze spielt. Sie bietet eine computational effiziente Alternative zu anderen Aktivierungsableitungen.
Verwendung des Rechners
Geben Sie eine beliebige reelle Zahl ein und klicken Sie auf 'Rechnen'. Die Ableitung ist für alle reellen Zahlen definiert und hat Werte zwischen 0 und 1.
Historischer Hintergrund
Die Softsign-Ableitung entwickelte sich als Teil der Suche nach besseren Gradientenfunktionen für neuronale Netze. Sie wurde als sanfte Alternative zu steileren Ableitungen wie der Sigmoid-Ableitung vorgeschlagen.
Eigenschaften und Anwendungen
Machine Learning Anwendungen
- Backpropagation in neuronalen Netzen
- Sanfte Gradientenberechnung
- Stabileres Training als steile Ableitungen
- Alternative zu Sigmoid-Ableitung
Computational Vorteile
- Einfache rationale Funktion
- Keine Exponentialfunktionen erforderlich
- Numerisch stabil für alle Eingaben
- Geringerer Rechenaufwand als Sigmoid-Ableitung
Mathematische Eigenschaften
- Maximum: softsign'(0) = 1 bei x = 0
- Symmetrie: softsign'(-x) = softsign'(x)
- Monotonie: Monoton fallend für |x| > 0
- Positivität: Immer positiv
Interessante Fakten
- Die einfache Form macht Backpropagation sehr effizient
- Maximum von 1 bei x = 0 bedeutet stärkste Lernrate in der Mitte
- Sanfterer Abfall als Sigmoid-Ableitung reduziert vanishing gradients
- Immer positive Werte vermeiden Sign-Switching-Probleme
Berechnungsbeispiele
Beispiel 1
softsign'(0) = 1
Maximum der Ableitung → Stärkste Lernrate
Beispiel 2
softsign'(1) = 0.25
Mittlere Eingabe → Moderate Lernrate
Beispiel 3
softsign'(3) ≈ 0.063
Große Eingabe → Sanfte Dämpfung
Vergleich mit anderen Ableitungen
vs. Sigmoid-Ableitung
Softsign' vs. σ'(x) = σ(x)(1-σ(x)):
- Höheres Maximum (1 vs. 0.25)
- Sanfterer Abfall für große |x|
- Einfachere Berechnung
- Weniger vanishing gradients
vs. Tanh-Ableitung
Softsign' vs. 1 - tanh²(x):
- Gleiches Maximum von 1
- Langsamere Sättigung
- Keine Exponentialfunktionen
- Bessere numerische Stabilität
Vor- und Nachteile
Vorteile
- Einfache, effiziente Berechnung
- Höheres Maximum als Sigmoid-Ableitung
- Sanfterer Gradient-Abfall
- Immer positive Werte
- Numerisch stabil
- Weniger vanishing gradients
Nachteile
- Weniger verbreitet als Sigmoid/Tanh-Ableitungen
- Kann bei sehr großen Netzen trotzdem sättigen
- Langsamer als ReLU (konstante Ableitung)
- Begrenzte empirische Studien
- Nicht so aggressiv wie moderne Aktivierungen
Auswirkungen auf das Training
Gradientenfluss
Die sanfte Form führt zu stabileren Gradienten:
Gleichmäßigere Gewichtsupdates durch sanfte Ableitung.
Konvergenz
Eigenschaften der Konvergenz:
- Stabilere Konvergenz als steile Ableitungen
- Weniger Oszillationen im Training
- Gleichmäßigere Lernrate über Zeit
- Robuster gegen Hyperparameter-Wahl
|
|
|
|