Derivative Sigmoid Funktion berechnen
Online Rechner zur Berechnung der Ableitung der Sigmoid Funktion - Essentiell für Backpropagation in neuronalen Netzen
Sigmoid Ableitung Rechner
Sigmoid Ableitung
Die σ'(x) oder Sigmoid-Ableitung ist essentiell für Gradient Descent und Backpropagation in neuronalen Netzen.
Glockenförmige Ableitungskurve
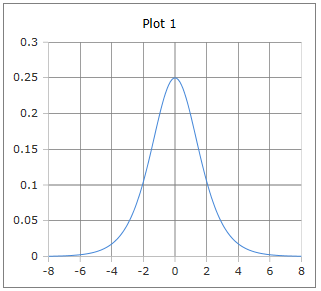
Die Kurve der derivativen Sigmoidfunktion: Glockenförmiger Verlauf mit Maximum bei x = 0.
Eigenschaften: Maximum 0.25 bei x = 0, symmetrisch, geht gegen 0 für große |x|.
|
|
Warum ist die Sigmoid-Ableitung glockenförmig?
Die glockenförmige Kurve der Sigmoid-Ableitung hat besondere Eigenschaften für das maschinelle Lernen:
- Maximum bei x = 0: Größte Änderungsrate in der Mitte
- Symmetrie: Gleiche Form links und rechts
- Begrenzte Werte: Zwischen 0 und 0.25
- Vanishing Gradients: Geht gegen 0 für große |x|
- Backpropagation: Bestimmt Lerngeschwindigkeit
- Optimierung: Wichtig für Gradientenabstieg
Kettenregel und Backpropagation
Die elegante Form σ'(x) = σ(x)(1-σ(x)) macht die Berechnung in neuronalen Netzen besonders effizient:
Da σ(x) bereits berechnet wurde, benötigt σ'(x) nur eine einfache Multiplikation, was die Backpropagation sehr effizient macht.
Formeln zur Sigmoid Ableitung
Elegante Form
Ausgedrückt durch die Sigmoid-Funktion selbst
Exponentialform
Direkte Ableitung der Exponentialform
Kettenregel Form
Für zusammengesetzte Funktionen
Alternative Form
Mit positiver Exponentialfunktion
Tanh Darstellung
Hyperbolische Sekansfunktion
Maximumseigenschaft
Maximum bei x = 0
Eigenschaften
Spezielle Werte
Definitionsbereich
Alle reellen Zahlen
Wertebereich
Zwischen 0 und 0.25
Anwendung
Backpropagation, Gradient Descent, Optimierung neuronaler Netze, Deep Learning.
Ausführliche Beschreibung der Sigmoid Ableitung
Mathematische Definition
Die Ableitung der Sigmoid-Funktion ist eine der elegantesten mathematischen Formeln im Machine Learning. Sie zeigt, wie sich die Sigmoid-Funktion an jedem Punkt ändert und ist fundamental für das Training neuronaler Netze durch Backpropagation.
Verwendung des Rechners
Geben Sie eine beliebige reelle Zahl ein und klicken Sie auf 'Rechnen'. Die Ableitung ist für alle reellen Zahlen definiert und hat Werte zwischen 0 und 0.25.
Historischer Hintergrund
Diese elegante Ableitungsformel wurde erstmals systematisch in den 1980er Jahren von Rumelhart, Hinton und Williams für die Backpropagation verwendet. Sie revolutionierte das Training mehrschichtiger neuronaler Netze.
Eigenschaften und Anwendungen
Machine Learning Anwendungen
- Backpropagation in neuronalen Netzen
- Gradient Descent Optimierung
- Fehlerrückführung in Deep Learning
- Adaptive Lernraten-Algorithmen
Numerische Eigenschaften
- Computational Efficiency (nutzt bereits berechnetes σ(x))
- Numerische Stabilität bei großen |x|
- Glatte, differenzierbare Funktion
- Begrenzte Werte verhindern Explosionen
Mathematische Eigenschaften
- Maximum: σ'(0) = 0.25 bei x = 0
- Symmetrie: σ'(-x) = σ'(x)
- Konvexität: Konkav für |x| < ln(2+√3)
- Asymptotik: Exponentieller Abfall für große |x|
Interessante Fakten
- Die elegante Form σ'(x) = σ(x)(1-σ(x)) macht Backpropagation effizient
- Das Maximum 0.25 bei x = 0 bestimmt die maximale Lerngeschwindigkeit
- Vanishing Gradients Problem: σ'(x) → 0 für große |x|
- Basis für modernere Aktivierungsfunktionen wie ReLU
Berechnungsbeispiele
Beispiel 1
σ'(0) = 0.25
Maximum der Ableitung → Beste Lernrate
Beispiel 2
σ'(2) ≈ 0.105
Positive Eingabe → Mittlere Lernrate
Beispiel 3
σ'(5) ≈ 0.007
Große Eingabe → Langsames Lernen
Rolle in der Backpropagation
Gradientenberechnung
In der Backpropagation wird die Sigmoid-Ableitung für die Kettenregel verwendet:
Dabei ist δⱼ der Fehler des Neurons j und wⱼₖ die Gewichte.
Gewichtsaktualisierung
Die Gewichte werden proportional zur Ableitung aktualisiert:
Wobei η die Lernrate und E die Fehlerfunktion ist.
Vanishing Gradients Problem
Problem
Für große |x| wird σ'(x) sehr klein, was zu langsamen Lernen führt:
- σ'(5) ≈ 0.007 (sehr langsam)
- σ'(10) ≈ 0.00005 (praktisch stillstand)
- Tief Netzwerke besonders betroffen
Lösungsansätze
Moderne Ansätze zur Lösung des Problems:
- ReLU Aktivierungsfunktionen
- Residual Connections (ResNet)
- Batch Normalization
- LSTM/GRU für Sequenzen
|
|
|
|