Bessel-J Funktion berechnen
Online Rechner zur Bessel-Funktion Jᵥ(z) der ersten Art - Klassische oszillierende Zylinderfunktion für Wellenprozesse
Bessel-J Funktion Rechner
Klassische Bessel-Funktion
Die Jᵥ(z) oder klassische Bessel-Funktion zeigt oszillierendes Verhalten und ist die Grundlage aller Zylinderfunktionen.
Bessel-J Funktionskurve
Mauszeiger auf der Grafik zeigt die Werte an.
Die klassische Bessel-Funktion zeigt charakteristische Oszillationen mit dämpfender Amplitude.
|
|
Charakteristische Oszillationen der Bessel-J Funktion
Die klassische Bessel-Funktion ist die ursprüngliche und wichtigste Zylinderfunktion:
- Periodische Oszillation: Jᵥ(z) oszilliert für große z
- Dämpfende Amplitude: Amplitude ~ 1/√z
- Unendliche Nullstellen: Regelmäßig verteilte Nullstellen
- Fundamentale Bedeutung: Basis aller anderen Bessel-Funktionen
- Physikalische Relevanz: Direkte Lösung der Wellengleichung
- Asymptotik: Jᵥ(z) ~ √(2/πz) cos(z - πν/2 - π/4)
Fundamentale Lösung in zylindrischen Koordinaten
Die Bessel-J Funktion ist die fundamentale Lösung der Bessel-Differentialgleichung:
Bessel-Differentialgleichung
Fundamentale DGL der Zylinderfunktionen
Allgemeine Lösung
J und Y bilden ein fundamentales Lösungssystem
Formeln zur Bessel-J Funktion
Reihenentwicklung
Fundamentale Potenzreihenentwicklung
Symmetrierelation
Für ganzzahlige ν
Asymptotische Form
Für große z (Hauptterm der asymptotischen Entwicklung)
Rekursionsformeln
Rekursionsrelationen für effiziente Berechnung
Integraldarstellung
Für ganzzahlige Ordnung n (Bessel-Integral)
Erzeugende Funktion
Laurent-Entwicklung der erzeugenden Funktion
Spezielle Werte
Wichtige Werte
Symmetrieeigenschaften
Für ganzzahlige n
Verhalten bei z = 0
Grenzverhalten im Ursprung
Nullstellen von J₀
Erste Nullstellen der Grundmode
Anwendungsgebiete
Membranschwingungen, Wellenleiter, akustische Resonatoren, Antennentheorie.
Bessel-J Oszillationsmuster
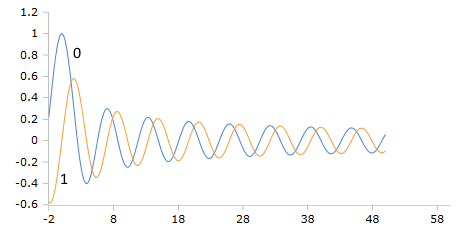
Bessel-J Funktionen (Ordnung 0,1)
Die klassischen Bessel-Funktionen zeigen charakteristische Oszillationen mit abnehmender Amplitude proportional zu 1/√z für große Argumente.
Charakteristische Eigenschaften
- J₀(z) startet bei 1, erste Nullstelle bei z ≈ 2.405
- J₁(z) startet bei 0, erste Nullstelle bei z ≈ 3.832
- Asymptotisch: ~ √(2/πz) cos(...)
- Periode der Oszillation ≈ 2π für große z
Ausführliche Beschreibung der Bessel-J Funktion
Mathematische Definition
Die klassische Bessel-Funktion Jᵥ(z) ist die fundamentale Lösung der Bessel-Differentialgleichung. Sie wurde ursprünglich von Friedrich Bessel bei der Analyse der Planetenbewegung entwickelt und ist heute die wichtigste Zylinderfunktion.
Verwendung des Rechners
Geben Sie die Ordnungszahl ν (ganze Zahl) und das Argument z (positive reelle Zahl) ein. Der Grafik-Stretch Parameter steuert die X-Achsen-Skalierung für optimale Oszillationsdarstellung.
Historischer Hintergrund
Friedrich Bessel (1784-1846) entwickelte diese Funktionen ursprünglich für astronomische Berechnungen. Die Funktionen erwiesen sich als fundamental für alle Probleme mit Zylindersymmetrie und sind heute unverzichtbar in Physik und Ingenieurwissenschaften.
Eigenschaften und Anwendungen
Physikalische Anwendungen
- Kreisförmige Membranschwingungen (Trommelfell, Lautsprecher)
- Elektromagnetische Wellen in zylindrischen Wellenleitern
- Akustische Resonatoren und Hohlraumresonatoren
- Beugung elektromagnetischer Wellen an Zylindern
Mathematische Eigenschaften
- Oszillierendes Verhalten mit dämpfender Amplitude
- Unendlich viele Nullstellen für ν ≥ 0
- Orthogonalitätsrelationen auf Intervallen
- Vollständiges Funktionensystem für zylindrische Probleme
Numerische Aspekte
- Stabilität: Numerisch stabil für alle reellen z ≥ 0
- Algorithmen: Verschiedene Methoden je nach z-Bereich
- Genauigkeit: Hohe Präzision durch optimierte Implementierungen
- Effizienz: Rekursionsformeln für benachbarte Ordnungen
Interessante Fakten
- J₀(z) beschreibt die Grundschwingung einer kreisförmigen Membran
- Die Nullstellen bestimmen Resonanzfrequenzen zylindrischer Hohlräume
- Bessel-Funktionen sind essentiell für die Fourier-Bessel-Transformation
- Sie ermöglichen die Lösung der Wellengleichung in zylindrischen Koordinaten
Berechnungsbeispiele und Oszillationsverhalten
Kleines Argument
z = 1:
J₀(1) ≈ 0.765
J₁(1) ≈ 0.440
Erste Nullstelle
z ≈ 2.405:
J₀(2.405) ≈ 0
Erste Nullstelle von J₀
Großes Argument
z = 20:
J₀(20) ≈ 0.167
Asymptotisches Verhalten
Physikalische Anwendungen im Detail
Membranschwingungen
Kreisförmige Membran:
u(r,φ,t) = J_m(k·r) cos(mφ) cos(ωt)
Resonanzen bei J_m(k·R) = 0
Beispiel: Trommelfell mit Radius R hat Grundfrequenz bei k·R = 2.405.
Elektromagnetische Wellen
Zylindrische Wellenleiter:
E_z ∝ J_m(k_c·r) e^(imφ) e^(ikz)
Cutoff bei J_m(k_c·a) = 0
Beispiel: Koaxialkabel und Hohlleiter nutzen diese Moden.
Nullstellen und spezielle Eigenschaften
Nullstellen der ersten Ordnungen
J₀(z) Nullstellen:
2.405, 5.520, 8.654, 11.792, 14.931, ...
J₁(z) Nullstellen:
3.832, 7.016, 10.173, 13.324, 16.471, ...
Asymptotik: Nullstellen folgen αₙ ≈ (n + ν/2 - 1/4)π für große n.
Asymptotisches Verhalten
Für große z:
Jᵥ(z) ~ √(2/πz) cos(z - νπ/2 - π/4)
Amplitude ~ 1/√z, Periode ≈ 2π
Eigenschaften: Dämpfende Oszillation mit konstanter Frequenz.
Orthogonalität und Fourierreihen
Orthogonalitätsrelation
Auf Intervall [0,R]:
für m ≠ n
Bedeutung: Ermöglicht Fourier-Bessel-Entwicklungen.
Fourier-Bessel-Reihe
Entwicklung einer Funktion f(r):
mit Koeffizienten A_n
Anwendung: Lösung von Randwertproblemen in Zylindern.
Numerische Berechnung und Algorithmen
Berechnungsmethoden
- Series Expansion: Für kleine |z| ≤ 8
- Asymptotic Expansion: Für große |z| ≥ 25
- Recurrence Relations: Für mittlere Bereiche
- Chebyshev Approximation: Für Übergangsbereiche
Software-Implementierungen
- GNU GSL: Hochpräzise Implementierungen
- Boost Math: C++ Template-Bibliothek
- SciPy: Python scipy.special.jv
- MATLAB: Built-in besselj Funktion
|
|
|
|