Sigmoid Funktion berechnen
Online Rechner und Formeln zur Sigmoid Funktion - Die wichtigste Aktivierungsfunktion in neuronalen Netzen
Sigmoid Funktion Rechner
Sigmoid (Logistische) Funktion
Die σ(x) oder logistische Funktion ist die wichtigste Aktivierungsfunktion in neuronalen Netzen und Machine Learning.
S-förmige Sigmoid Kurve
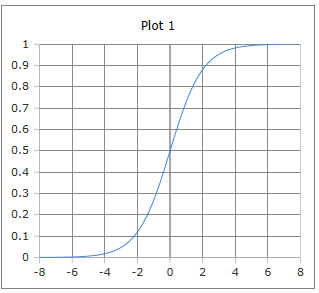
Die logistische Kurve der Sigmoidfunktion: S-förmiger Verlauf mit Werten zwischen 0 und 1.
Eigenschaften: Glatt differenzierbar, monoton steigend, Symmetrie um (0, 0.5).
|
|
Was macht die Sigmoid-Funktion besonders?
Die S-förmige Kurve der Sigmoid-Funktion macht sie ideal für viele Anwendungen:
- Glatte Übergänge: Keine sprunghaften Änderungen
- Begrenzte Ausgabe: Immer zwischen 0 und 1
- Differenzierbarkeit: Überall glatt ableitbar
- Wahrscheinlichkeits-Interpretation: Perfekt für binäre Klassifikation
- Biologische Inspiration: Ähnelt Neuronenaktivierung
- Mathematische Eleganz: Einfache, aber mächtige Formel
Formeln zur Sigmoid Funktion
Standardform
Klassische logistische Funktion
Alternative Form
Äquivalente Exponentialform
Tanh Darstellung
Hyperbolische Tangensform
Ableitung
Elegante Ableitungsformel
Generalisierte Form
Mit Parametern L, k, x₀
Logit Umkehrung
Sigmoid und Logit sind invers
Eigenschaften
Spezielle Werte
Definitionsbereich
Alle reellen Zahlen
Wertebereich
Immer zwischen 0 und 1
Anwendung
Neuronale Netze, Machine Learning, logistische Regression, Wahrscheinlichkeitsmodelle.
Ausführliche Beschreibung der Sigmoid Funktion
Mathematische Definition
Die Sigmoid-Funktion, auch als logistische Funktion bekannt, ist eine der wichtigsten S-förmigen Funktionen in der Mathematik. Sie bildet reelle Zahlen auf das Intervall (0,1) ab und ist die Grundlage vieler Machine Learning Algorithmen.
Verwendung des Rechners
Geben Sie eine beliebige reelle Zahl ein und klicken Sie auf 'Rechnen'. Die Funktion ist für alle reellen Zahlen definiert und liefert Werte zwischen 0 und 1.
Historischer Hintergrund
Die logistische Funktion wurde ursprünglich von Pierre François Verhulst 1838 zur Beschreibung von Populationswachstum entwickelt. In den 1940er Jahren wurde sie von McCulloch und Pitts als Aktivierungsfunktion für künstliche Neuronen eingeführt.
Eigenschaften und Anwendungen
Machine Learning Anwendungen
- Aktivierungsfunktion in neuronalen Netzen
- Binäre Klassifikation (Output-Layer)
- Logistische Regression
- Gradient Descent Optimierung
Wissenschaftliche Anwendungen
- Populationsdynamik (Wachstumsmodelle)
- Epidemiologie (Ausbreitungsmodelle)
- Psychologie (Lernkurven)
- Ökonomie (Adoptionsmodelle)
Mathematische Eigenschaften
- Monotonie: Streng monoton steigend
- Symmetrie: σ(-x) = 1 - σ(x)
- Differenzierbarkeit: Unendlich oft differenzierbar
- Grenzwerte: lim_{x→∞} σ(x) = 1, lim_{x→-∞} σ(x) = 0
Interessante Fakten
- Die Ableitung hat die elegante Form σ'(x) = σ(x)(1-σ(x))
- Maximum der Ableitung bei x = 0 mit σ'(0) = 0.25
- Basis der logistischen Regression und vieler Deep Learning Modelle
- Kann durch das Vanishing Gradient Problem begrenzt werden
Berechnungsbeispiele
Beispiel 1
σ(0) = 0.5
Neutrale Eingabe → 50% Wahrscheinlichkeit
Beispiel 2
σ(2) ≈ 0.881
Positive Eingabe → Hohe Aktivierung
Beispiel 3
σ(-2) ≈ 0.119
Negative Eingabe → Niedrige Aktivierung
Rolle in Neuronalen Netzen
Aktivierungsfunktion
In neuronalen Netzen transformiert die Sigmoid-Funktion die Summe der gewichteten Eingaben:
Dabei sind wᵢ die Gewichte, xᵢ die Eingaben und b der Bias.
Backpropagation
Die elegante Ableitung macht Gradientenberechnung einfach:
Dies ermöglicht effizientes Training durch Backpropagation.
Vor- und Nachteile
Vorteile
- Glatte, differenzierbare Funktion
- Ausgabe zwischen 0 und 1 (Wahrscheinlichkeits-Interpretation)
- Einfache Ableitung
- Biologisch plausibel
Nachteile
- Vanishing Gradient Problem bei tiefen Netzen
- Nicht null-zentriert (kann Konvergenz verlangsamen)
- Rechenintensiv (Exponentialfunktion)
- Sättigung bei großen |x| Werten
|
|
|
|