Bessel-Ke Funktion berechnen
Online Rechner zur exponentiell skalierten modifizierten Bessel-Funktion Keᵥ(z) der zweiten Art - Numerisch stabile Lösung für große Argumente
Bessel-Ke Funktion Rechner
Exponentiell skalierte K-Funktion
Die Keᵥ(z) oder exponentiell skalierte modifizierte Bessel-Funktion bietet numerische Stabilität für extrem kleine Werte.
Bessel-Ke Funktionskurve
Mauszeiger auf der Grafik zeigt die Werte an.
Die exponentiell skalierte Form eliminiert numerische Probleme bei großen z.
|
|
Warum exponentielle Skalierung bei der K-Funktion?
Die exponentiell skalierte modifizierte Bessel-K Funktion löst spezielle numerische Herausforderungen:
- Extremer Abfall: Verhindert Unterläufe bei großen z
- Exponentieller Faktor: Keᵥ(z) = e^z Kᵥ(z)
- Numerische Robustheit: Stabile Berechnung für alle z-Bereiche
- Wissenschaftliches Computing: Standard in numerischen Bibliotheken
- Präzisionserhaltung: Vermeidet Rundungsfehler
- Algorithmus-Effizienz: Optimierte Implementierungen
Numerische Vorteile der exponentiellen Skalierung
Die exponentiell skalierte K-Funktion bietet entscheidende numerische Verbesserungen:
Problem bei Standard Kᵥ(z)
- Exponentieller Abfall ~ e^(-z)
- Unterlauf bei z > ~700
- Verlust der numerischen Präzision
Lösung durch Keᵥ(z)
- Skalierter Wertebereich ohne Unterlauf
- Stabile Berechnung für beliebig große z
- Erhaltene relative Genauigkeit
Formeln zur Bessel-Ke Funktion
Definition
Exponentiell skalierte modifizierte Bessel-Funktion
Beziehung zu Kᵥ
Umkehrung der Skalierung
Integraldarstellung
Skalierte Integralform für Re(z) > 0
Asymptotische Form
Für große z (ohne exponentiellen Abfall)
Rekursionsformel
Gleiche Rekursion wie unscaled Version
Symmetrieeigenschaft
Symmetrie bezüglich der Ordnung
Verhalten bei z → 0
Skalierte Singularität im Ursprung
Spezielle Werte
Wichtige Werte
Symmetrieeigenschaften
Für alle reellen ν
Singularität bei z = 0
Für alle ν ≥ 0 (skaliert)
Verhalten bei z → ∞
Algebraischer Abfall (skaliert)
Anwendungsgebiete
Numerische Stabilität, große Parameter, wissenschaftliches Computing, Präzisionsalgorithmen.
Bessel-Ke vs. Bessel-K Vergleich
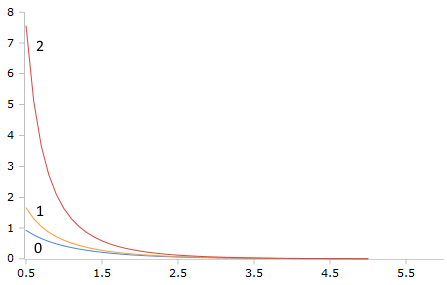
Bessel-Ke Funktionen (Ordnung 0,1,2)
Die exponentiell skalierten K-Funktionen zeigen algebraisches Abfallverhalten ohne numerische Unterläufe auch bei sehr großen z-Werten.
Charakteristische Eigenschaften
- Keᵥ(z) → ∞ für z → 0⁺ (skalierte Singularität)
- Keᵥ(z) ~ √(π/2z) für z → ∞
- Asymptotisch: ~ 1/√z statt e^(-z)
- Numerisch stabil für alle z-Bereiche
Ausführliche Beschreibung der Bessel-Ke Funktion
Mathematische Definition
Die exponentiell skalierte modifizierte Bessel-Funktion Keᵥ(z) ist eine numerisch stabilisierte Version der modifizierten Bessel-K Funktion. Sie wurde entwickelt, um die numerischen Probleme des extremen exponentiellen Abfalls zu lösen.
Verwendung des Rechners
Geben Sie die Ordnungszahl ν (ganze Zahl) und das Argument z (positive reelle Zahl) ein. Die Ke-Version ist besonders für große z-Werte und numerische Stabilität geeignet.
Numerischer Hintergrund
Die Entwicklung der exponentiell skalierten K-Funktionen war eine Antwort auf die extremen numerischen Herausforderungen bei der Berechnung von Kᵥ(z) für große z. Während Kᵥ(z) exponentiell gegen 0 abfällt und Unterläufe verursacht, bleibt Keᵥ(z) numerisch handhabbar.
Eigenschaften und Anwendungen
Numerische Anwendungen
- Scientific Computing mit extremen Parametern
- Hochpräzisions-Numerik (IEEE floating-point)
- Simulation physikalischer Systeme bei großen Entfernungen
- Statistische Berechnungen mit weiten Parameterbereichen
Mathematische Eigenschaften
- Algebraisches Abfallverhalten ~ 1/√z
- Singularität bei z = 0 (skaliert)
- Symmetrie: Ke₋ᵥ(z) = Keᵥ(z)
- Monotonie-Eigenschaften ähnlich der Standard-K-Version
Implementierungsaspekte
- Bibliotheken: Standard in modernen Math-Libraries
- Präzision: Erhaltene Genauigkeit bei großen z
- Performance: Optimierte Algorithmen verfügbar
- Robustheit: Vermeidet numerische Unterläufe
Interessante Fakten
- Die Ke-Funktionen sind essential in modernen numerischen Bibliotheken
- Für große z: Keᵥ(z) ≈ √(π/2z) statt Kᵥ(z) ≈ √(π/2z) e^(-z)
- Algorithmen verwenden oft spezielle Rekursionsformeln für Effizienz
- Wichtig in numerischen Simulationen mit extremen Parametern
Berechnungsbeispiele und Skalierungsvergleiche
Kleines Argument
z = 1:
K₀(1) ≈ 0.421
Ke₀(1) ≈ 1.144
Mittleres Argument
z = 10:
K₀(10) ≈ 1.78×10⁻⁵
Ke₀(10) ≈ 0.399
Großes Argument
z = 100:
K₀(100) → Unterlauf
Ke₀(100) ≈ 0.126
Computational Vergleich: Standard vs. Skaliert
Standard Kᵥ(z) Probleme
Exponentieller Abfall:
K₀(50) ≈ 3.4 × 10⁻²³
K₀(100) ≈ 4.7 × 10⁻⁴⁵
K₀(700) → Unterlauf
Problem: Numerische Unterläufe begrenzen den nutzbaren Bereich erheblich.
Keᵥ(z) Lösung
Kontrolliertes Verhalten:
Ke₀(50) ≈ 0.178
Ke₀(100) ≈ 0.126
Ke₀(700) ≈ 0.048
Vorteil: Stabile Berechnung für beliebig große Argumente.
Physikalische Interpretation und Anwendungen
Wärmeleitung (skaliert)
Skalierte Temperaturverteilung:
T_scaled(r) = A Ke₀(r/λ)
Numerisch stabil für große Entfernungen
Vorteil: Berechnung auch bei sehr großen Entfernungen möglich.
Elektromagnetische Felder
Skalierte Feldabfälle:
E_scaled(r) ∝ Ke₀(r/δ)
Präzise Berechnung bei großen Entfernungen
Anwendung: Fernfeldberechnungen und Abschirmungseffekte.
Numerische Berechnung und Algorithmen
Berechnungsmethoden
- Series Expansion: Für kleine z (skalierte Koeffizienten)
- Asymptotic Expansion: Für große z (vereinfacht durch Skalierung)
- Recurrence Relations: Stabil für alle z-Bereiche
- Continued Fractions: Optimierte Konvergenz
Software-Implementierungen
- GNU GSL: Optimierte Ke-Funktionen
- Boost Math: C++ Template-Bibliothek mit Skalierung
- SciPy: Python scipy.special.kve
- MATLAB: Built-in besselk mit Scaling-Option
|
|
|
|