Dodekaeder Rechner
Onlinerechner und Formeln zur Berechnung der Eigenschaften eines Dodekaeders
Dodekaeder Rechner
Das Dodekaeder
Das Dodekaeder ist ein platonischer Körper mit 12 gleichmäßigen Fünfecken und dem Goldenen Schnitt.
Platonischer Körper Eigenschaften
Der Goldene Körper: 12 regelmäßige Fünfecke mit dem Goldenen Schnitt
Dodekaeder Struktur
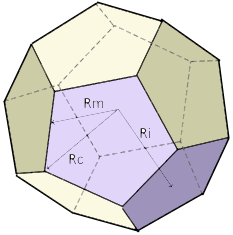
Der platonische Körper mit dem Goldenen Schnitt.
12 regelmäßige Fünfecke.
Was ist ein Dodekaeder?
Das Dodekaeder ist einer der fünf platonischen Körper:
- Definition: Körper mit 12 regelmäßigen Fünfecken
- Platonischer Körper: Einer der fünf regelmäßigen Polyeder
- Flächen: 12 kongruente regelmäßige Fünfecke
- Ecken: 20 Ecken insgesamt
- Kanten: 30 Kanten
- Goldener Schnitt: Basis aller Proportionen
Geometrische Eigenschaften des Dodekaeders
Das Dodekaeder zeigt die Vollendung der platonischen Symmetrie:
Grundparameter
- Flächen: 12 regelmäßige Fünfecke
- Ecken: 20 Ecken
- Kanten: 30 Kanten (alle gleich lang)
- Euler-Charakteristik: V - E + F = 20 - 30 + 12 = 2
Besondere Eigenschaften
- Goldener Schnitt: Basis aller Proportionen
- Ikosaeder-Dual: Dualkörper zum Ikosaeder
- Platonisch: Einer der fünf regulären Polyeder
- Pentagonal: Alle Flächen sind Fünfecke
Mathematische Beziehungen
Das Dodekaeder folgt den Gesetzen des Goldenen Schnitts:
Volumen-Formel
Enthält den Goldenen Schnitt φ = (1+√5)/2. Elegant und harmonisch.
Oberflächen-Formel
12 regelmäßige Fünfecke. Mit √25+10√5 Beziehung.
Anwendungen des Dodekaeders
Dodekaeder finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Geodätische Kuppeln
- Sakrale Architektur
- Harmonische Raumaufteilung
- Goldener Schnitt in Proportionen
Wissenschaft & Technik
- Kristallographische Strukturen
- Virusstrukturen
- Fullerene-Verwandte
- Symmetrie-Studien
Bildung & Lehre
- Geometrie-Unterricht
- Platonische Körper Studien
- Goldener Schnitt Demonstration
- Symmetrie-Lehre
Kunst & Design
- Geometrische Skulpturen
- Harmonische Proportionen
- Dekorative Objekte
- Spielwürfel (W12)
Formeln zur Berechnung eines Dodekaeders
Volumen (V)
Volumen mit dem Goldenen Schnitt φ
Oberfläche (S)
12 regelmäßige Fünfecke
Eckenradius (Rc)
Umkugelradius mit Goldenem Schnitt
Kantenradius (Rm)
Mittelkugelradius
Innenradius (Ri)
Inkugelradius
Diagonale & Höhe
Durchmesser und Höhe
Der Goldene Schnitt φ
φ = (1+√5)/2 ≈ 1.618
Harmonische Verhältnisse
Perfektion in Symmetrie
Alle Dodekaeder-Proportionen basieren auf dem Goldenen Schnitt φ
Berechnungsbeispiel für ein Dodekaeder
Gegeben
Gesucht: Alle Eigenschaften des Dodekaeders
1. Volumen-Berechnung
Für a = 10:
\[V = \frac{10^3}{4}(15+7\sqrt{5})\] \[V ≈ 250 \cdot 30.652\] \[V ≈ 7663.0\]Das Volumen beträgt etwa 7663 Volumeneinheiten
2. Oberflächen-Berechnung
Für a = 10:
\[S = 3 \cdot 10^2 \sqrt{25+10\sqrt{5}}\] \[S ≈ 300 \cdot 6.882\] \[S ≈ 2064.6\]Die Oberfläche beträgt etwa 2065 Flächeneinheiten
3. Radien-Berechnung
Für a = 10:
\[R_c ≈ 1.401 \cdot 10 = 14.01\] \[R_m ≈ 1.309 \cdot 10 = 13.09\] \[R_i ≈ 1.113 \cdot 10 = 11.13\]Die Radien mit dem Goldenen Schnitt
4. Das perfekte Dodekaeder
Das Dodekaeder mit perfekter Goldener-Schnitt-Symmetrie
Das Dodekaeder: Der Goldene Platonische Körper
Das Dodekaeder ist der faszinierendste der fünf platonischen Körper und verkörpert die Vollendung der geometrischen Harmonie. Mit seinen 12 regelmäßigen Fünfecken, 20 Ecken und 30 Kanten ist es ein Meisterwerk der Symmetrie, das vollständig auf dem Goldenen Schnitt φ = (1+√5)/2 ≈ 1.618 basiert. Jede Proportion, jeder Winkel und jede Beziehung in diesem Körper folgt den harmonischen Gesetzen des Goldenen Schnitts, was ihn zu einem Symbol für Perfektion und natürliche Schönheit macht.
Die Vollendung der platonischen Symmetrie
Das Dodekaeder zeigt die höchste Form der geometrischen Vollendung:
- Goldener Schnitt: Alle Proportionen basieren auf φ = (1+√5)/2
- Regelmäßige Fünfecke: 12 kongruente pentagoale Flächen
- Ikosaeder-Dual: Dualkörper zum Ikosaeder
- Platonische Perfektion: Einer der fünf regulären Polyeder
- Harmonische Winkel: Alle Winkel folgen φ-Beziehungen
- Natürliche Präsenz: Grundlage vieler natürlicher Strukturen
- Kristallographische Bedeutung: Vorlage für Quasikristalle
Mathematische Vollendung
Goldener-Schnitt-Perfektion
Alle Formeln des Dodekaeders enthalten den Goldenen Schnitt φ als fundamentalen Baustein, was zu einer einzigartigen harmonischen Struktur führt.
Pentagoale Symmetrie
Die 12 regelmäßigen Fünfecke erzeugen eine fünfzählige Rotationssymmetrie, die in der Natur weit verbreitet ist.
Duale Beziehungen
Als Dual zum Ikosaeder zeigt das Dodekaeder die tiefe Verbindung zwischen den platonischen Körpern.
Universelle Harmonie
Von Molekularstrukturen bis zu kosmischen Mustern - das Dodekaeder repräsentiert universelle Ordnungsprinzipien.
Zusammenfassung
Das Dodekaeder verkörpert die Vollendung der geometrischen Harmonie und steht als Krone der platonischen Körper da. Seine Struktur aus 12 regelmäßigen Fünfecken, vollständig durchdrungen vom Goldenen Schnitt, macht es zu einem faszinierenden Studienobjekt für Mathematiker, Naturwissenschaftler und Künstler. Von der reinen Geometrie über Kristallstrukturen bis hin zu architektonischen Meisterwerken zeigt das Dodekaeder, wie mathematische Perfektion und natürliche Schönheit untrennbar miteinander verbunden sind. Seine φ-basierten Formeln offenbaren die tiefe Verbindung zwischen Mathematik und Natur und machen es zu einem Symbol für die universelle Ordnung und Harmonie des Kosmos. In einer Welt voller Komplexität steht das Dodekaeder als leuchtendes Beispiel für die Kraft der geometrischen Vollendung.
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder