Würfel Rechner
Rechner und Formeln zur Berechnung des Volumens, der Oberfläche und Diagonalen eines Würfels
Würfel Rechner
Der Würfel (Hexaeder)
Der Würfel ist der bekannteste platonische Körper mit 6 perfekten Quadraten und einfachsten Beziehungen.
Platonischer Körper Eigenschaften
Der vertraute Würfel: 6 perfekte Quadrate mit den einfachsten mathematischen Beziehungen
Würfel Struktur
Der bekannteste platonische Körper.
6 perfekte Quadrate.
|
|
Was ist ein Würfel (Hexaeder)?
Der Würfel ist der bekannteste der fünf platonischen Körper:
- Definition: Körper mit 6 kongruenten Quadraten
- Platonischer Körper: Der vertrauteste der fünf regulären Polyeder
- Flächen: 6 identische Quadrate
- Ecken: 8 Ecken insgesamt
- Kanten: 12 Kanten (alle gleich lang)
- Dual: Dual zum Oktaeder
Geometrische Eigenschaften des Würfels
Der Würfel zeigt die Vollendung der quadratischen Symmetrie:
Grundparameter
- Flächen: 6 kongruente Quadrate
- Ecken: 8 Ecken
- Kanten: 12 Kanten (alle gleich lang)
- Euler-Charakteristik: V - E + F = 8 - 12 + 6 = 2
Besondere Eigenschaften
- Hexaeder: 6-flächiger Körper
- Oktaeder-Dual: Dual zum Oktaeder
- Platonisch: Einfachste kubische Form
- Symmetrie: Höchste kubische Symmetrie
Mathematische Beziehungen
Der Würfel folgt den einfachsten geometrischen Gesetzen:
Volumen-Formel
Dritte Potenz der Seitenlänge. Die einfachste Volumen-Formel.
Oberflächen-Formel
6 identische Quadrate. Perfekte Symmetrie.
Anwendungen des Würfels
Würfel finden Anwendung in unzähligen Bereichen:
Architektur & Bauwesen
- Grundform für Gebäude
- Modulare Konstruktionen
- Raumaufteilung
- Strukturelle Grundelemente
Wissenschaft & Technik
- Kristallstrukturen
- 3D-Koordinatensysteme
- Computergrafik
- Materialwissenschaft
Bildung & Lehre
- Grundlagen der Geometrie
- Räumliches Vorstellungsvermögen
- Volumen- und Flächenberechnung
- Koordinatensysteme
Alltag & Design
- Spielwürfel (W6)
- Verpackungen und Container
- Möbeldesign
- Architektonische Elemente
Formeln zur Berechnung eines Würfels
Seitenlänge (a)
Aus allen anderen Parametern berechenbar
Volumen (V)
Die einfachste Volumen-Formel
Oberfläche (S)
6 identische Quadrate
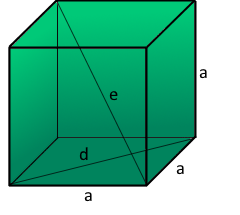
Flächendiagonale (d)
Diagonale einer Seitenfläche
Raumdiagonale (e)
Diagonale durch den ganzen Würfel
Umkugelradius (R)
Radius der umschreibenden Kugel
Die einfachen Beziehungen des Würfels
V = a³
S = 6a²
d = a√2
e = a√3
Der Würfel zeigt die einfachsten und elegantesten geometrischen Beziehungen
Berechnungsbeispiel für einen Würfel
Gegeben
Gesucht: Alle Eigenschaften des Würfels
1. Volumen-Berechnung
Für a = 5:
\[V = a^3 = 5^3\] \[V = 125\]Das Volumen beträgt exakt 125 Volumeneinheiten
2. Oberflächen-Berechnung
Für a = 5:
\[S = 6a^2 = 6 \cdot 5^2\] \[S = 6 \cdot 25 = 150\]Die Oberfläche beträgt exakt 150 Flächeneinheiten
3. Diagonalen-Berechnung
Für a = 5:
\[d = 5\sqrt{2} ≈ 7.07\] \[e = 5\sqrt{3} ≈ 8.66\]Flächendiagonale ≈ 7.07, Raumdiagonale ≈ 8.66
4. Der perfekte Würfel
Der Würfel mit perfekter kubischer Symmetrie
Der Würfel: Der vertraute Platonische Körper
Der Würfel (auch Hexaeder genannt) ist der vertrauteste und bekannteste aller platonischen Körper. Mit seinen 6 identischen Quadraten, 8 Ecken und 12 Kanten verkörpert er die Vollendung der geometrischen Einfachheit und Symmetrie. Seine mathematischen Beziehungen sind die elementarsten: das Volumen ist einfach a³, die Oberfläche 6a², und seine Diagonalen folgen den grundlegenden Quadratwurzeln √2 und √3. Als Dualkörper zum Oktaeder zeigt er die perfekte Balance zwischen kubischer und oktaedrischer Symmetrie.
Die Vollendung der kubischen Symmetrie
Der Würfel zeigt die fundamentalen Prinzipien der kubischen Geometrie:
- Hexaeder: Sechs identische quadratische Flächen
- Kubische Symmetrie: Höchste kubische Punktsymmetrie
- Oktaeder-Dual: Perfekte duale Beziehung zum Oktaeder
- Elementare Formeln: Einfachste mathematische Beziehungen
- Koordinaten-Basis: Grundlage des kartesischen Systems
- Universelle Form: Grundform in Architektur und Design
- Praktische Perfektion: Ideal für Verpackung und Lagerung
Mathematische Klarheit
Elementare Einfachheit
Die Formeln des Würfels sind die einfachsten aller platonischen Körper: a³ für das Volumen, 6a² für die Oberfläche.
Quadratische Perfektion
Sechs identische Quadrate bilden eine perfekt symmetrische dreidimensionale Form.
Duale Balance
Als Dual zum Oktaeder zeigt der Würfel die harmonische Balance zwischen verschiedenen Symmetrietypen.
Universelle Bedeutung
Der Würfel ist die Grundform für unzählige praktische Anwendungen in Architektur, Design und Technik.
Zusammenfassung
Der Würfel verkörpert die Essenz der geometrischen Klarheit und steht als universelle Grundform da. Seine Struktur aus 6 identischen Quadraten, beschrieben durch die einfachsten mathematischen Beziehungen, macht ihn zum zugänglichsten aller platonischen Körper. Von der Grundschulmathematik über Architektur bis hin zur Computergrafik zeigt der Würfel, wie geometrische Einfachheit und praktische Anwendbarkeit perfekt harmonieren. Seine elementaren Formeln - a³, 6a², a√2, a√3 - sind so fundamental, dass sie die Basis für das Verständnis komplexerer Geometrien bilden. Als Dualkörper zum Oktaeder demonstriert er die schöne Balance verschiedener Symmetrietypen und bleibt ein zeitloses Symbol für die Kraft der geometrischen Ordnung und die Schönheit der mathematischen Einfachheit.
|
|
|
|
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder