ReLU (Leaky) Funktion berechnen
Online Rechner und Formeln zur ReLU (Rectified Linear Unit) Aktivierungsfunktion - Die moderne Alternative zu Sigmoid
ReLU Funktion Rechner
Rectified Linear Unit (ReLU)
Die f(x) = max(0, x) oder Leaky-ReLU: f(x) = max(αx, x) ist eine der wichtigsten Aktivierungsfunktionen in Deep Learning.
ReLU Kurve
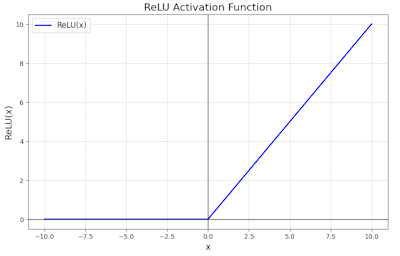
ReLU-Kurve: Null für negative Eingaben, linear für positive Werte.
Leaky-ReLU: Erlaubt kleine negative Steigung für besseres Training.
|
|
Was macht ReLU besonders?
Die ReLU-Funktion revolutionierte Deep Learning durch ihre Einfachheit und Effektivität:
- Rechnerisch effizient: Nur ein Vergleich und keine Exponentialfunktion
- Sparsame Aktivierung: Viele Neuronen können "aus" sein (f(x)=0)
- Starke Gradienten: Keine Sättigung bei positiven Werten
- Bessere Konvergenz: Training ist schneller und stabiler
- Biologisch inspiriert: Ähnelt tatsächlicher Neuronenaktivierung
- Variationen: Leaky-ReLU, ELU, GELU für spezielle Anwendungen
Formeln zur ReLU Funktion
Standard ReLU
Einfachste und schnellste Aktivierungsfunktion
Leaky ReLU
Verhindert Probleme bei negativen Eingaben
ReLU Ableitung
Konstante Gradienten (kein Vanishing Gradient)
Leaky ReLU Ableitung
Kleine Steigung bei negativen Werten
Parametric ReLU (PReLU)
Lernbar: αᵢ wird während Training angepasst
ELU (Exponential Linear Unit)
Glatte Funktion mit besserer Stabilität
Eigenschaften
Spezielle Werte
Definitionsbereich
Alle reellen Zahlen
Wertebereich
Unbegrenzt nach oben, 0 nach unten
Anwendung
Convolutional Neural Networks (CNN), Recurrent Neural Networks (RNN), Moderne Deep Learning Architekturen.
Ausführliche Beschreibung der ReLU Funktion
Mathematische Definition
Die ReLU (Rectified Linear Unit) Funktion ist eine der am häufigsten verwendeten Aktivierungsfunktionen in modernem Deep Learning. Sie ist einfach zu berechnen, numerisch stabil und führt zu besserer Konvergenz während des Trainings.
Verwendung des Rechners
Geben Sie eine beliebige reelle Zahl ein und optional einen Leaky-Parameter α. Der Rechner berechnet sowohl die Funktionswerte als auch die Ableitungen für die Backpropagation.
Historischer Hintergrund
ReLU wurde 2011 von Geoffrey Hinton popularisiert und führte zu einem Durchbruch in Deep Learning. Im Gegensatz zu Sigmoid und Tanh ermöglicht ReLU tiefere Netzwerke ohne Vanishing Gradient Probleme.
Eigenschaften und Variationen
Deep Learning Anwendungen
- Convolutional Neural Networks (CNNs) für Bildverarbeitung
- Recurrent Neural Networks (RNNs, LSTMs)
- Transformer und Attention Mechanismen
- Generative Adversarial Networks (GANs)
ReLU Variationen
- Leaky ReLU: Ermöglicht kleine negative Werte
- Parametric ReLU (PReLU): α wird trainiert
- ELU (Exponential Linear Unit): Glatte Variante
- GELU: Gaussian Error Linear Unit (in Transformers)
Mathematische Eigenschaften
- Monotonie: Monoton steigend
- Nicht-Linearität: Piecewise linear
- Sparsität: Viele Ausgaben sind exakt 0
- Gradient: 0 oder 1 (kein Vanishing)
Interessante Fakten
- ReLU ermöglichte erfolgreiches Training von Netzwerken mit 8+ Hidden Layers
- 50% der Aktivierungen sind typischerweise 0 (Sparsität)
- Neuronale Netzwerke lernen schneller mit ReLU als mit Sigmoid
- Dead ReLU Problem: Neuronen können "tot" sein und nicht mehr aktivieren
Berechnungsbeispiele
Beispiel 1: Standard ReLU
ReLU(0) = 0
ReLU(2) = 2
ReLU(-2) = 0
Beispiel 2: Leaky ReLU (α=0.1)
f(0) = 0
f(2) = 2
f(-2) = -0.2
Beispiel 3: Ableitungen
f'(2) = 1 (steiler Aufstieg)
f'(-2) = 0 (kein Gradient)
Leaky: f'(-2) = 0.1 (kleine Steigung)
Rolle in Neuronalen Netzen
Aktivierungsfunktion
In neuronalen Netzen transformiert die ReLU-Funktion die Summe der gewichteten Eingaben:
Dies ermöglicht nicht-lineare Entscheidungsgrenzen während Training und Inference.
Backpropagation
Die einfache Ableitung ermöglicht effizientes Gradient Descent:
Keine Exponentialfunktion = schneller und stabiler!
Vorteile und Nachteile
Vorteile
- Extrem schnell zu berechnen (nur ein Vergleich)
- Kein Vanishing Gradient Problem bei tiefen Netzen
- Führt zu sparsamen Aktivierungen
- Biologisch realistisch
- Einfach zu implementieren
Nachteile
- Dead ReLU Problem (Neuronen können "tot" sein)
- Unbegrenzte Ausgaben bei sehr großen Eingaben
- Nicht differenzierbar bei x=0
- Nicht-zentriert um 0
- Erfordert Careful Weight Initialization
|
|
|
|