Aktivitätsauswahlproblem
Rechner zum optimalen Scheduling von Aktivitäten (ISMP)
Intervall-Scheduling-Maximierungsproblem: Finde die maximale Anzahl nicht-überlappender Aktivitäten
Activity Selection Rechner
Aktivitätsauswahl-Problem
Das Aktivitätsauswahlproblem ermittelt die maximale Anzahl von Aktivitäten, die ohne zeitliche Überlappung durchgeführt werden können.
Scheduling Visualisierung
Beispiel: Standarddaten

Zeitachsen-Darstellung der Aktivitäten
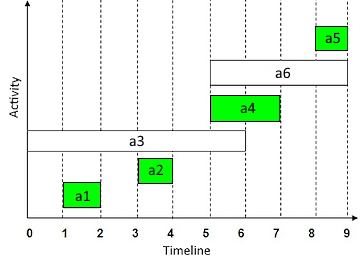
Optimale Auswahl ohne Überlappungen
Greedy-Algorithmus
- Sortiere nach Endzeiten
- Wähle früheste Endzeit
- Überspringe überlappende Aktivitäten
- Wiederhole bis alle geprüft
|
|
Greedy-Algorithmus für Activity Selection
Der Greedy-Algorithmus löst das Aktivitätsauswahlproblem optimal durch eine einfache Strategie:
Schritt 1: Sortierung
Aktivitäten nach aufsteigenden Endzeiten ordnen
Schritt 2: Greedy-Auswahl
Keine Überlappung mit letzter gewählter Aktivität
Mathematische Formulierung und Beispiele
Problem-Definition
Maximiere die Anzahl ausgewählter Aktivitäten ohne Überlappung
Greedy-Algorithmus Pseudocode
Zeitkomplexität: O(n log n) für Sortierung + O(n) für Auswahl
Schritt-für-Schritt Beispiel
Gegeben: Aktivitäten mit Start- und Endzeiten
| Aktivität | Startzeit (s) | Endzeit (f) | Dauer |
|---|---|---|---|
| A₁ | 1 | 2 | 1 |
| A₂ | 3 | 4 | 1 |
| A₃ | 0 | 6 | 6 |
| A₄ | 5 | 7 | 2 |
| A₅ | 8 | 9 | 1 |
| A₆ | 5 | 9 | 4 |
Lösungsschritte:
1. Sortierung nach Endzeiten: A₁(f=2) → A₂(f=4) → A₃(f=6) → A₄(f=7) → A₅(f=9) → A₆(f=9)
2. A₁ wählen: Endzeit = 2
3. A₂ prüfen: Start(3) ≥ 2 ✓ → A₂ wählen, Endzeit = 4
4. A₃ prüfen: Start(0) < 4 ✗ → überspringen
5. A₄ prüfen: Start(5) ≥ 4 ✓ → A₄ wählen, Endzeit = 7
6. A₅ prüfen: Start(8) ≥ 7 ✓ → A₅ wählen, Endzeit = 9
7. A₆ prüfen: Start(5) < 7 ✗ → überspringen
Ergebnis: {A₁, A₂, A₄, A₅} - 4 Aktivitäten
Optimalitätsbeweis (Greedy Choice Property)
Theorem: Der Greedy-Algorithmus (früheste Endzeit zuerst) liefert eine optimale Lösung.
Beweis: Sei A* eine optimale Lösung und A die Greedy-Lösung. Falls die erste Aktivität in A* nicht die früheste Endzeit hat, kann sie durch die früheste ersetzt werden, ohne die Optimalität zu verlieren.
Activity Selection Referenz
Standard-Beispiel
Komplexität
Zeit: O(n log n)
Speicher: O(1)
Sortierung: O(n log n)
Auswahl: O(n)
Greedy-Strategien
✓ Früheste Endzeit: optimal
✗ Kürzeste Dauer: nicht optimal
✗ Wenigste Konflikte: nicht optimal
✗ Früheste Startzeit: nicht optimal
Anwendungen
Scheduling: Ressourcenplanung
Rooms: Raumbelegung
Machines: Maschinenauslastung
Events: Veranstaltungsplanung
Aktivitätsauswahlproblem - Detaillierte Beschreibung
Problem-Definition
Das Aktivitätsauswahlproblem ist ein klassisches Optimierungsproblem der Informatik und Operations Research. Gegeben sind n Aktivitäten mit jeweiliger Start- und Endzeit. Das Ziel ist es, die maximale Anzahl von Aktivitäten auszuwählen, die sich zeitlich nicht überlappen.
• Aktivität i: Startzeit s_i, Endzeit f_i
• Zwei Aktivitäten überlappen, wenn ihre Zeitintervalle sich schneiden
• Ziel: Maximiere |S| mit S ⊆ {1,2,...,n}
• Nebenbedingung: Keine zwei Aktivitäten in S überlappen
Greedy-Algorithmus
Der Greedy-Algorithmus löst das Problem optimal durch eine einfache Heuristik: Wähle immer die Aktivität mit der frühesten Endzeit, die nicht mit bereits gewählten Aktivitäten kollidiert. Diese Strategie ist überraschenderweise optimal.
Warum "Früheste Endzeit"?
Eine Aktivität mit früherer Endzeit lässt mehr Raum für zukünftige Aktivitäten. Dies maximiert die Wahlmöglichkeiten für die verbleibende Zeit.
Praktische Anwendungen
Activity Selection findet Anwendung in vielen realen Scheduling-Problemen: von der Raumbelegung in Universitäten über die Maschinenauslastung in Fabriken bis hin zur optimalen Nutzung von Rundfunkfrequenzen.
• Konferenzraum-Buchungen
• Produktionsplanung
• Personalschichtplanung
• Ressourcenallokation
Algorithmus-Analyse
Die Zeitkomplexität des Algorithmus wird hauptsächlich durch die Sortierung der Aktivitäten nach Endzeiten bestimmt: O(n log n). Die eigentliche Auswahl erfolgt in linearer Zeit O(n).
Optimality Proof
Der Beweis der Optimalität erfolgt durch Austausch-Argument: Jede optimale Lösung kann in eine Greedy-Lösung transformiert werden, ohne die Anzahl der gewählten Aktivitäten zu reduzieren.
Praktische Beispiele und Varianten
Konferenzraum-Scheduling
Problem: Meetings optimal planen
Input: Meeting-Zeiten
Lösung: Maximale Meetings
Nutzen: Raum-Effizienz
Maschinen-Scheduling
Problem: Jobs auf Maschine
Input: Bearbeitungszeiten
Lösung: Maximale Auslastung
Nutzen: Durchsatz-Optimierung
Frequenz-Zuteilung
Problem: Sendeslots verteilen
Input: Übertragungszeiten
Lösung: Interferenz-frei
Nutzen: Spektrum-Effizienz
Erweiterte Varianten
- Gewichtetes Problem: Aktivitäten haben unterschiedliche Prioritäten
- Multi-Maschinen: Mehrere parallele Ressourcen
- Online-Version: Aktivitäten kommen sequenziell an
- Deadlines: Aktivitäten haben harte Deadlines
- Setup-Zeiten: Umrüstzeiten zwischen Aktivitäten
- Ressourcen-Constraints: Zusätzliche Ressourcenbeschränkungen
|
|
|
|