Exponentiell skalierte Bessel-Ie Funktion für komplexe Zahlen

Berechnung der exponentiell skalierten modifizierten Bessel-Funktion \(I_e(z) = e^{-|z|} I_\nu(z)\) der ersten Art

Bessel-Ie Funktionsrechner

Exponentiell skalierte Bessel-Funktion \(I_e(z)\)

Die exponentiell skalierte Bessel-Funktion \(I_e(z) = e^{-|z|} I_\nu(z)\) verhindert numerische Überläufe bei großen Argumenten und ist besonders nützlich für numerische Berechnungen mit großen Werten.

Komplexes Argument z = a + bi

Realteil (a)

Imaginärteil (b)

Ordnungszahl ν

Ganzzahlige oder rationale Ordnung der Bessel-Funktion

Dezimalstellen

Berechnungsergebnis

\(I_e(z)\) =

Bessel-Ie Eigenschaften

Skalierung

Exponentiell

Faktor: \(e^{-|z|}\)

Verhindert Overflow

Basis

Bessel-I

Typ: \(I_\nu(z)\)

Modifizierte Funktion

Ordnung

ν ∈ ℝ

Beliebige reelle Zahl

Ganzzahlig oder rational

Argument

z ∈ ℂ

Komplex: a+bi

Reell- und Imaginärteil

Wichtige Eigenschaften

Numerisch stabile Berechnung bei großen |z|
Verhindert exponentiellen Overflow
Definiert als: \(I_e(z) = e^{-|z|} I_\nu(z)\)
Asymptotisch: \(I_e(z) \sim \frac{1}{\sqrt{2\pi|z|}}\) für |z| → ∞

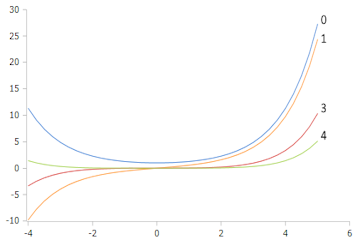
Plot der Bessel-I Funktion (vor exponentieller Skalierung)

Definition der exponentiell skalierten Bessel-Funktion

Die exponentiell skalierte modifizierte Bessel-Funktion \(I_e(z)\) ist definiert als:

Skalierte Definition

\[I_e(z) = e^{-|z|} I_\nu(z) = e^{-|z|} \sum_{m=0}^{\infty} \frac{1}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Exponentiell skalierte Version zur Vermeidung numerischer Überläufe

Numerische Stabilität

\[|I_e(z)| \leq \frac{C}{\sqrt{|z|}}\]

Begrenzt für große |z|, verhindert Overflow

Beziehung zur Bessel-I

\[I_\nu(z) = e^{|z|} I_e(z)\]

Rücktransformation zur ursprünglichen Funktion

Wichtige Eigenschaften der skalierten Bessel-Funktion

Asymptotisches Verhalten

\[I_e(z) \sim \frac{1}{\sqrt{2\pi|z|}} \quad \text{für } |z| \to \infty\]

Konstantes asymptotisches Verhalten ohne exponentielles Wachstum

Numerische Vorteile

\[\max|I_e(z)| < \infty \quad \text{für alle } z\]

Begrenzte Werte verhindern Overflow-Probleme

Skalierungsfaktor

\[s(z) = e^{-|z|} = e^{-\sqrt{\text{Re}(z)^2 + \text{Im}(z)^2}}\]

Exponentieller Dämpfungsfaktor basierend auf dem Betrag von z

Rekurrenzrelationen

\[I_{e,\nu-1}(z) - I_{e,\nu+1}(z) = \frac{2\nu}{z} I_{e,\nu}(z)\]

Skalierte Rekurrenzrelationen gelten analog

Anwendungen der skalierten Bessel-Funktion

Numerische Analyse

Große Argumente Overflow-Vermeidung Stabile Algorithmen Präzise Berechnung

Wissenschaftliches Rechnen

Monte-Carlo-Methoden:
Statistische Simulationen
Zufallsprozesse

Finanzmodelle:
Optionsbewertung
Risikomodellierung

Signalverarbeitung

Filterdesign

Spektralanalyse

Beamforming

Physikalische Modelle

Diffusionsgleichungen

Wärmeleitungsmodelle

Quantenfeldtheorie

Streutheorie

Exponentiell skalierte Bessel-Funktionen - Detaillierte Beschreibung

Numerische Stabilität

Die exponentiell skalierte Bessel-Funktion \(I_e(z)\) wurde speziell entwickelt, um die numerischen Probleme der gewöhnlichen modifizierten Bessel-Funktion \(I_\nu(z)\) bei großen Argumenten zu lösen.

Problemstellung:
• \(I_\nu(z)\) wächst exponentiell für große |z|
• Numerische Überläufe bei |z| > 700
• Präzisionsverlust in Berechnungen
• Instabile Algorithmen

Lösungsansatz

Durch die Definition \(I_e(z) = e^{-|z|} I_\nu(z)\) wird der exponentiell wachsende Teil "herausdividiert", sodass die resultierende Funktion numerisch stabil bleibt.

Vorteile der Skalierung

Ohne Skalierung: \(I_\nu(100)\) ≈ 10⁴³ (Overflow)
Mit Skalierung: \(I_{e,\nu}(100)\) ≈ 0.056 (stabil)

Mathematische Eigenschaften

Die skalierte Funktion behält alle wichtigen mathematischen Eigenschaften der ursprünglichen Bessel-Funktion bei, ist aber numerisch viel stabiler.

Erhaltene Eigenschaften:
• Rekurrenzrelationen bleiben gültig
• Differentialgleichungen analog
• Symmetriebeziehungen bestehen fort
• Integraldarstellungen möglich

Implementierung

In der numerischen Praxis wird die skalierte Version verwendet und das Ergebnis bei Bedarf zurücktransformiert:

\[I_\nu(z) = e^{|z|} \cdot I_e(z)\]

Rücktransformation nur wenn explizit benötigt

Computerimplementierung

Moderne Bibliotheken verwenden die skalierte Version automatisch und handhaben die Skalierung transparent für den Benutzer.

Vergleich: Skaliert vs. Unskaliert

Unskalierte Bessel-I Funktion

Definition: \(I_\nu(z)\)
Verhalten: Exponentielles Wachstum
Probleme: Overflow bei großen |z|
Grenze: |z| ≲ 700 (double precision)

Skalierte Bessel-Ie Funktion

Definition: \(I_e(z) = e^{-|z|} I_\nu(z)\)
Verhalten: Asymptotisch konstant
Vorteile: Kein Overflow
Bereich: Alle |z| (praktisch unbegrenzt)

Praktische Anwendungsrichtlinien

Kleine |z| ≤ 10: Beide Versionen verwendbar
Mittlere |z| ≤ 100: Skalierte Version empfohlen
Große |z| > 100: Nur skalierte Version verwenden

Iterative Algorithmen: Immer skalierte Version
Wissenschaftliche Bibliotheken: Automatische Wahl
Spezielle Funktionen: Skalierung transparent

Bessel-Funktionen - Vollständige Definitionen und Skalierung

Modifizierte Bessel-Funktionen

Die modifizierte Bessel-Funktion erster Art n-ter Ordnung ist definiert als:

\[I_{\nu}(z) = \sum_{m=0}^{\infty} \frac{1}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Die exponentiell skalierte Version ist:

\[I_e(z) = e^{-|z|} I_{\nu}(z)\]

Die modifizierte Bessel-Funktion zweiter Art ist:

\[K_{\nu}(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_{\nu}(z)}{\sin(\nu \pi)}\]

Gewöhnliche Bessel-Funktionen

Die Bessel-Funktion erster Gattung n-ter Ordnung ist definiert als:

\[J_{\nu}(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Die Bessel-Funktion zweiter Gattung n-ter Ordnung ist:

\[Y_{\nu}(z) = \frac{J_{\nu}(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)}\]

Anwendungsgebiete

Die exponentiell skalierte Bessel-Funktion ist besonders wichtig in der numerischen Mathematik, Signalverarbeitung, Quantenphysik und allen Bereichen, wo große Argumentwerte auftreten können. Sie ermöglicht stabile Berechnungen auch bei extremen Parameterbereichen.

Weitere Komplexe Funktionen

Betrag / Absolutwert • Division • Exponent • Konjugierte • Logarithmus zur Basis 10 • Multiplikation • Natürlicher Logarithmus • Polarform • Quadratwurzel • Wurzel • Potenz • Reziprok • Winkel •
Cosh • Sinh • Tanh •
Acos • Asin • Atan • Cos • Sin • Tan •
Airy Funktion • Abgeleitete Airy Funktion •
Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye