Modifizierte Bessel-K Funktion für komplexe Zahlen

Berechnung der modifizierten Bessel-Funktion \(K_\nu(z)\) der zweiten Art mit exponentiell abklingendem Verhalten

Bessel-K Funktionsrechner

Modifizierte Bessel-Funktion \(K_\nu(z)\) zweiter Art

Die modifizierte Bessel-Funktion zweiter Art \(K_\nu(z)\) zeigt exponentiell abklingendes Verhalten und ist singulär am Ursprung. Sie ist eine Lösung der modifizierten Bessel-Differentialgleichung.

Komplexes Argument z = a + bi

Realteil (a)

Imaginärteil (b)

Ordnungszahl ν

Ganzzahlige oder rationale Ordnung der Bessel-Funktion

Dezimalstellen

Berechnungsergebnis

\(K_\nu(z)\) =

Bessel-K Eigenschaften

Verhalten

Abklingend

Exponentiell → 0

Für große |z|

Art

Zweite Art

Typ: \(K_\nu\)

Singulär bei z=0

Ordnung

ν ∈ ℝ

Beliebige reelle Zahl

Ganzzahlig oder rational

Argument

z ∈ ℂ

Komplex: a+bi

Reell- und Imaginärteil

Wichtige Eigenschaften

Lösung der modifizierten Bessel-Differentialgleichung
Exponentiell abklingendes Verhalten: \(K_\nu(z) \sim \sqrt{\frac{\pi}{2z}} e^{-z}\)
Singularität am Ursprung: \(K_\nu(0) = \infty\) (außer spezielle Fälle)
Symmetrierelation: \(K_{-\nu}(z) = K_\nu(z)\)

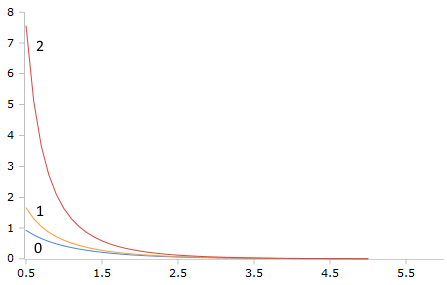
Plot der Bessel-K Funktion mit den Ordnungszahlen 0, 1 und 2

Definition der modifizierten Bessel-K Funktion zweiter Art

Die modifizierte Bessel-Funktion zweiter Art \(K_\nu(z)\) ist definiert durch:

Standarddefinition

\[K_\nu(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_\nu(z)}{\sin(\nu \pi)}\]

Definition durch die modifizierten Bessel-Funktionen erster Art \(I_\nu(z)\) und \(I_{-\nu}(z)\)

Modifizierte Bessel-DGL

\[z^2 \frac{d^2w}{dz^2} + z \frac{dw}{dz} - (z^2 + \nu^2)w = 0\]

Differentialgleichung mit Lösung \(w = K_\nu(z)\)

Integraldarstellung

\[K_\nu(z) = \int_0^\infty e^{-z\cosh t} \cosh(\nu t) \, dt\]

Gültig für \(\text{Re}(z) > 0\)

Wichtige Eigenschaften der Bessel-K Funktion

Asymptotisches Verhalten

\[K_\nu(z) \sim \sqrt{\frac{\pi}{2z}} e^{-z}\]

Exponentiell abklingend für große |z|

Verhalten am Ursprung

\[K_0(z) \sim -\ln(z)\] \[K_\nu(z) \sim \frac{\Gamma(\nu)}{2}\left(\frac{2}{z}\right)^\nu \text{ für } \nu > 0\]

Singulär am Ursprung für alle ν

Symmetrierelationen

\[K_{-\nu}(z) = K_\nu(z)\]

Symmetrie bezüglich der Ordnung

Rekurrenzrelationen

\[K_{\nu-1}(z) - K_{\nu+1}(z) = -\frac{2\nu}{z} K_\nu(z)\] \[K_{\nu-1}(z) + K_{\nu+1}(z) = -2 K_\nu'(z)\]

Beziehungen zwischen verschiedenen Ordnungen

Anwendungen der Bessel-K Funktion

Wärmeleitung

Zylindrische Körper Stationäre Zustände Temperaturverteilung Diffusionsprozesse

Potentialtheorie

Elektrostatik:
Zylindrische Ladungen
Abschirmung

Gravitation:
Massenpotentiale
Zylindrische Verteilungen

Stochastik & Finanzen

Optionspreismodelle

Brownsche Bewegung

Varianz-Gamma-Prozesse

Quantenphysik

Yukawa-Potential

Streutheorie

Abschirmeffekte

Tunneleffekte

Modifizierte Bessel-K Funktionen - Detaillierte Beschreibung

Exponentiell abklingendes Verhalten

Die modifizierte Bessel-Funktion zweiter Art \(K_\nu(z)\) unterscheidet sich fundamental von \(I_\nu(z)\) durch ihr exponentiell abklingendes Verhalten.

Charakteristische Eigenschaften:
• Exponentielles Abklingen für große |z|
• Singularität am Ursprung (z=0)
• Immer positiv für reelle positive z
• Beschränkt für große Argumente

Historischer Hintergrund

Die modifizierten Bessel-Funktionen wurden aus den gewöhnlichen Bessel-Funktionen durch die Transformation \(z \to iz\) entwickelt. Die K-Funktionen sind besonders wichtig für Probleme mit exponentiell abklingenden Lösungen.

Physikalische Interpretation

\(K_0(r)\) beschreibt das stationäre Temperaturfeld einer unendlich langen linienförmigen Wärmequelle in einem unbegrenzten Medium. Die Funktion fällt exponentiell mit dem Abstand r ab.

Numerische Aspekte

Die K-Funktionen sind numerisch gut handhabbar, da sie für große Argumente exponentiell abklingen und keine Oszillationen aufweisen.

Numerische Eigenschaften:
• Keine Overflow-Probleme bei großen |z|
• Stabile Berechnungen möglich
• Rekurrenz vorwärts stabil
• Singularität am Ursprung erfordert Vorsicht

Berechnungsmethoden

Verschiedene numerische Methoden werden je nach Argumentbereich verwendet:

Kleine |z|: Reihenentwicklung um z=0
Mittlere |z|: Integraldarstellung
Große |z|: Asymptotische Entwicklung \(\sim e^{-z}/\sqrt{z}\)
Komplexe z: Spezielle Algorithmen erforderlich

Spezielle Werte

Einige wichtige Grenzwerte:
\(\lim_{z \to 0^+} K_0(z) = +\infty\) (logarithmische Singularität)
\(\lim_{z \to \infty} K_\nu(z) = 0\) (exponentielles Abklingen)

Vergleich: Bessel-K vs. Bessel-I

Modifizierte Bessel-K Funktion (zweite Art)

Definition: \(K_\nu(z)\) über \(I_{\pm\nu}(z)\)
Verhalten: Exponentiell abklingend
DGL: \(z^2w'' + zw' - (z^2+\nu^2)w = 0\)
Asymptotik: \(\sim \sqrt{\frac{\pi}{2z}} e^{-z}\)
Ursprung: Singulär bei z=0

Modifizierte Bessel-I Funktion (erste Art)

Definition: \(I_\nu(z) = i^{-\nu} J_\nu(iz)\)
Verhalten: Exponentiell wachsend
DGL: \(z^2w'' + zw' - (z^2+\nu^2)w = 0\)
Asymptotik: \(\sim \frac{e^z}{\sqrt{2\pi z}}\)
Ursprung: Endlich bei z=0

Anwendungsrichtlinien

Wärmeleitung: K für Abkühlung, Wärmeabfluss
Diffusion: K für Konzentrations-Abnahme
Yukawa-Potential: K-Funktion beschreibt Abschirmung

Unbegrenzte Gebiete: K für Randverhalten im Unendlichen
Stationäre Zustände: K für exponentielles Abklingen
Finanzmathematik: K in Optionspreismodellen

Bessel-Funktionen - Vollständige Definitionen und Beziehungen

Gewöhnliche Bessel-Funktionen

Die Bessel-Funktion erster Art n-ter Ordnung ist definiert als:

\[J_{\nu}(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Die Bessel-Funktion zweiter Art (Neumann-Funktion) ist:

\[Y_{\nu}(z) = \frac{J_{\nu}(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)}\]

Anwendungen der J-Funktionen

Gewöhnliche Bessel-Funktionen für oszillierende Phänomene mit Zylindersymmetrie: Schwingungen, elektromagnetische Wellen, Quantenmechanik.

Modifizierte Bessel-Funktionen

Die modifizierte Bessel-Funktion erster Art ist definiert als:

\[I_{\nu}(z) = i^{-\nu} J_{\nu}(iz)\]

Die modifizierte Bessel-Funktion zweiter Art ist:

\[K_{\nu}(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_{\nu}(z)}{\sin(\nu \pi)}\]

Wronskische Determinante

Für die modifizierten Bessel-Funktionen gilt:
\(W[I_\nu(z), K_\nu(z)] = I_\nu(z)K_\nu'(z) - I_\nu'(z)K_\nu(z) = -\frac{1}{z}\)

Dies zeigt, dass \(I_\nu\) und \(K_\nu\) linear unabhängige Lösungen der modifizierten Bessel-Differentialgleichung sind.

Weitere Komplexe Funktionen

Betrag / Absolutwert • Division • Exponent • Konjugierte • Logarithmus zur Basis 10 • Multiplikation • Natürlicher Logarithmus • Polarform • Quadratwurzel • Wurzel • Potenz • Reziprok • Winkel •
Cosh • Sinh • Tanh •
Acos • Asin • Atan • Cos • Sin • Tan •
Airy Funktion • Abgeleitete Airy Funktion •
Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye