Sinc - Kardinalsinus eines Winkels berechnen

Online calculator for calculating the unnormalized cardinal sine


The calculator on this page calculates the cardinal sine for real numbers. Trigonometric functions for complex numbers can be found in the complex numbers section.

Enter the angle whose cardinal sine should be calculated and click on the Calculate button. The unit of measurement can be switched between degrees and radians.


Cardinal sine calculator

Input
Angle
Unit of measure
Decimal places
Result
Cardinal sine
Cardinal sine curve
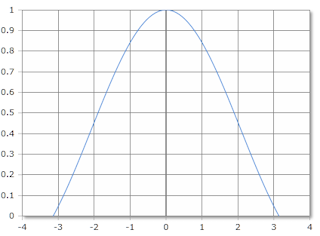
Cardinal sine, scale in radians

Description


The cardinal sine (sinus cardinalis) is an analytical function. The norm is not uniformly defined, especially in English-speaking countries, sinc is used for both both the normalized and unnormalized variants are used.

Here the non-standard version is implemented as shown in the following formula:

Kardinalsinus

In information theory and digital signal processing, the standardized form is mostly used:

Spaltfunktion

Input


The argument is given as a real number in degrees (-180°..+180°) or radians (-π..+π). The unit of measurement used is set using the Degrees or Radians menu


Result


Sinc returns a result in the range 0 to 1.



IT Functions

Decimal, Hex, Bin, Octal conversion • Shift bits left or right • Set a bit • Clear a bit • Bitwise AND • Bitwise OR • Bitwise exclusive OR

Special functions

Airy • Derivative Airy • Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye • Spherical-Bessel-J • Spherical-Bessel-Y • Hankel • Beta • Incomplete Beta • Incomplete Inverse Beta • Binomial Coefficient • Binomial Coefficient Logarithm • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Struve table • Modified Struve • Modified Struve table • Riemann Zeta

Hyperbolic functions

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Degree to Radian • Radian to Degree

Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?