Tan - Calculate Tangent
Online calculator for calculating the tangent of an angle
Tangent Calculator
Instructions
Enter the angle whose tangent you want to calculate, select the unit of measure (degrees or radians) and click Calculate.
Tangent - Overview
Value Range
The angle is given in degrees (full circle = 360°) or radians (full circle = 2·π).
Note: The tangent is undefined at 90°, 270° (or π/2, 3π/2 in radians) where cos(α) = 0.
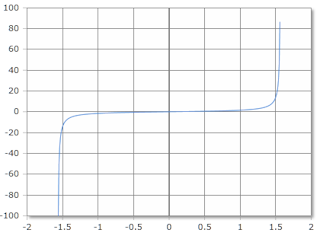
Tangent, scale in radians
Definition in Triangle
The tangent of an angle α corresponds to the ratio of the opposite side to the adjacent side in a right triangle.
\(\displaystyle \tan(\alpha) = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{a}{b} = \frac{\sin(\alpha)}{\cos(\alpha)} \)

Important Values
- \( \tan(0°) = 0 \)
- \( \tan(30°) = \frac{1}{\sqrt{3}} \approx 0.577 \)
- \( \tan(45°) = 1 \)
- \( \tan(60°) = \sqrt{3} \approx 1.732 \)
- \( \tan(90°) = \) undefined (∞)
- \( \tan(180°) = 0 \)
|
|
Description of the Tangent
Fundamentals
The tangent is one of the fundamental trigonometric functions. In a right triangle, the tangent of an angle α is the ratio of the opposite side to the adjacent side.
Definition:
\(\displaystyle \tan(\alpha) = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{a}{b} \)
\(\displaystyle \tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} \)
Properties
The tangent function has several important properties:
- Periodic: tan(α + 180°) = tan(α)
- Odd function: tan(-α) = -tan(α)
- Undefined: At 90° + n·180° (where cos(α) = 0)
- Range: All real numbers (-∞, +∞)
- Domain: All real numbers except 90° + n·180° (n integer)
Relationship to Other Functions
Tangent is related to other trigonometric functions:
\(\displaystyle \tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} \)
\(\displaystyle \tan(\alpha) = \frac{1}{\cot(\alpha)} \)
\(\displaystyle 1 + \tan^2(\alpha) = \sec^2(\alpha) \)
Detailed Examples
Example 1: Calculate Tangent
Given:
A right triangle with:
- Opposite side (to α): \( a = 3 \text{ cm} \)
- Adjacent side: \( b = 4 \text{ cm} \)
Calculation:
\(\displaystyle \tan(\alpha) = \frac{3}{4} = 0.75 \)
To find the angle: \( \alpha = \arctan(0.75) \approx 36.87° \)
Example 2: Known Angles
Important tangent values:
| \( \tan(0°) \) | = | 0 |
| \( \tan(30°) \) | = | \( \frac{1}{\sqrt{3}} \approx 0.577 \) |
| \( \tan(45°) \) | = | 1 |
| \( \tan(60°) \) | = | \( \sqrt{3} \approx 1.732 \) |
| \( \tan(120°) \) | = | \( -\sqrt{3} \approx -1.732 \) |
| \( \tan(180°) \) | = | 0 |
Example 3: Practical Application
Task:
A road has an incline of 15°. How much does the road rise over a horizontal distance of 100 m?
Solution:
\(\displaystyle \text{Rise} = 100 \cdot \tan(15°) \approx 100 \cdot 0.268 = 26.8 \text{ m} \)
Conversion
From degrees to radians:
\(\displaystyle \text{Radians} = \frac{\text{Degrees} \cdot \pi}{180°} \)
Mathematical Properties
- Period: 180° or π (radians)
- Symmetry: Odd function: tan(-α) = -tan(α)
- Asymptotes: Vertical at 90°, 270°, ...
- Zeros: At 0°, ±180°, ±360°, ...
- Slope interpretation: tan(α) represents the slope of a line
- Pythagorean identity: 1 + tan²(α) = sec²(α)
- Addition formulas:
- \( \tan(\alpha + \beta) = \frac{\tan\alpha + \tan\beta}{1 - \tan\alpha\tan\beta} \)
Practical Applications
- Engineering: Slope and gradient calculations
- Architecture: Roof pitch and stair design
- Navigation: Bearing and course calculations
- Surveying: Height and distance measurements
- Physics: Inclined plane problems
- Civil engineering: Road and railway gradients
- Computer graphics: Rotation and perspective
- Trigonometry: Solving triangles
Important Note
The tangent function is undefined at angles where the cosine equals zero (90°, 270°, ... or π/2, 3π/2, ...). At these points, the function approaches positive or negative infinity. The tangent can be expressed as tan(α) = sin(α)/cos(α). Unlike sine and cosine, the tangent can take any real value from -∞ to +∞. The function has a period of 180° (or π radians), which is half the period of sine and cosine. The tangent is particularly useful for calculating slopes and gradients, as tan(α) directly gives the rise/run ratio. In the unit circle, tan(α) represents the length of the line segment from the point (1,0) to where the line through the origin at angle α intersects the vertical tangent line x = 1.
|
|