ACsc - arccosecant (inverse cosecant)
Online calculator for calculating the arc cosecant (inverse cosecant)
The calculator on this page calculates the inverse cosecant for real numbers. Trigonometric functions for complex numbers can be found in the complex numbers section.
To calculate, enter the value of the cosecant whose angle should be calculated and click on the Calculate button. The unit of measurement for the result can be switched between degrees and radians
|
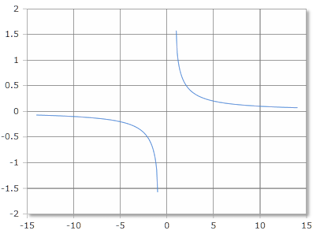
Inverse cosecant, scale in radians
Input
The value of the argument must be between -infinity ... -1 or 1 ... infinity.
Result
The result is given in degrees (range = -90° to +90°) or radians (range = -π/2 to +π/2). The unit of measurement used is set to degrees or radians at the top of the menu.
IT Functions
Decimal, Hex, Bin, Octal conversion • Shift bits left or right • Set a bit • Clear a bit • Bitwise AND • Bitwise OR • Bitwise exclusive ORSpecial functions
Airy • Derivative Airy • Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye • Spherical-Bessel-J • Spherical-Bessel-Y • Hankel • Beta • Incomplete Beta • Incomplete Inverse Beta • Binomial Coefficient • Binomial Coefficient Logarithm • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Struve table • Modified Struve • Modified Struve table • Riemann ZetaHyperbolic functions
ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • TanhTrigonometrische Funktionen
ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Degree to Radian • Radian to Degree
|
|