Inverse Hyperbolic Cotangent

Online calculator for calculating the angle to the inverse hyperbolic cotangent

ACoth Calculator

Domain Restriction

The ACoth(x) or inverse hyperbolic cotangent shows inverse function behavior with domain |x| > 1.

Value must be greater than 1 or less than -1
Results
Angle:

ACoth Function Curve

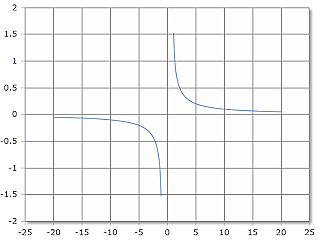
Curve of the ACoth function

The ACoth function has two separate branches with a gap at [-1, 1].
Domain: (-∞, -1) ∪ (1, ∞), Range: ℝ

Inverse Function Behavior of ACoth

The inverse hyperbolic cotangent function exhibits characteristic inverse properties:

  • Domain: (-∞, -1) ∪ (1, ∞) (|x| > 1)
  • Range: ℝ (all real numbers)
  • Discontinuity: Gap at [-1, 1]
  • Inverse: Coth(ACoth(x)) = x for |x| > 1
  • Branches: Two separate monotonic branches
  • Asymptotes: Vertical at x = ±1

Logarithmic Representation of ACoth Function

The inverse hyperbolic cotangent function is expressed through logarithmic functions:

Basic Formula
\[\text{ACoth}(x) = \frac{1}{2} \ln\left(\frac{x + 1}{x - 1}\right)\]

Natural logarithm expression for |x| > 1

Inverse Relation
\[\coth(\text{ACoth}(x)) = x\]

For |x| > 1

Formulas for the ACoth Function

Definition
\[\text{ACoth}(x) = \frac{1}{2} \ln\left(\frac{x + 1}{x - 1}\right)\]

Natural logarithm expression for |x| > 1

Inverse Relation
\[\coth(\text{ACoth}(x)) = x \text{ for } |x| > 1\] \[\text{ACoth}(\coth(y)) = y \text{ for } y \neq 0\]

Fundamental inverse function properties

Derivative
\[\frac{d}{dx} \text{ACoth}(x) = \frac{1}{1 - x^2}\]

First derivative for |x| > 1

Domain Restriction
\[|x| > 1 \text{ (required for real values)}\]

Returns NaN for -1 ≤ x ≤ 1

Branch Behavior
\[\text{ACoth}(x) > 0 \text{ for } x > 1\] \[\text{ACoth}(x) < 0 \text{ for } x < -1\]

Two separate monotonic branches

Special Values

Important Values
ACoth(2) ≈ 0.549 ACoth(-2) ≈ -0.549 ACoth(3) ≈ 0.347
Invalid Range
\[-1 \leq x \leq 1: \text{NaN}\]

Function undefined in interval [-1, 1]

Asymptotes
\[x = \pm 1: \text{vertical asymptotes}\]

Function approaches ±∞ at x = ±1

Properties
  • Inverse function
  • Two separate branches
  • Odd function symmetry
  • Logarithmic singularities
Branch Limits
\[\lim_{x \to 1^+} \text{ACoth}(x) = +\infty\] \[\lim_{x \to -1^-} \text{ACoth}(x) = -\infty\]

Divergent behavior at boundaries

Applications

Statistical mechanics, signal processing, inverse hyperbolic problems, mathematical physics.

Detailed Description of the ACoth Function

Definition and Input

The inverse hyperbolic cotangent function ACoth(x) is the inverse function of the hyperbolic cotangent. It exhibits characteristic two-branch behavior with a restricted domain.

Critical Property: The ACoth function requires |x| > 1 for real values!
Input

The argument must be less than -1 or greater than 1. Values in the interval [-1, 1] return NaN (not a valid number).

Result

The result is given in degrees (full circle = 360°) or radians (full circle = 2π). The unit of measurement used is set using the Degrees or Radians menu.

Using the Calculator

Enter a value with absolute value greater than 1. The ACoth function calculates the angle whose hyperbolic cotangent equals the input value.

Mathematical Properties

Function Properties
  • Domain: (-∞, -1) ∪ (1, ∞) (|x| > 1)
  • Range: ℝ (all real numbers)
  • Discontinuity: Gap at interval [-1, 1]
  • Symmetry: Odd function ACoth(-x) = -ACoth(x)
Two-Branch Properties
  • Positive branch for x > 1
  • Negative branch for x < -1
  • Vertical asymptotes at x = ±1
  • Each branch is monotonically decreasing
Applications
  • Statistical Mechanics: Phase transitions
  • Signal Processing: Inverse transformations
  • Mathematical Physics: Soliton theory
  • Engineering: Control system analysis
Practical Notes
  • Domain restriction: |x| > 1 (undefined for |x| ≤ 1)
  • Two separate branches with gap at [-1, 1]
  • Odd function: ACoth(-x) = -ACoth(x)
  • Inverse relation: Coth(ACoth(x)) = x for |x| > 1

Calculation Examples

Positive Branch

ACoth(2) ≈ 0.549

ACoth(3) ≈ 0.347

ACoth(5) ≈ 0.203

Negative Branch

ACoth(-2) ≈ -0.549

ACoth(-3) ≈ -0.347

ACoth(-5) ≈ -0.203

Invalid Inputs

ACoth(0) = NaN

ACoth(0.5) = NaN

-1 ≤ x ≤ 1: undefined

Mathematical and Physical Applications

Statistical Mechanics

Phase Transitions:

Critical behavior analysis

Two-state system models

Application: Ising model and magnetic phase transitions.

Signal Processing

Inverse Transforms:

Nonlinear signal recovery

Two-branch inverse mapping

Example: Inverse hyperbolic transformations in communications.

Important Mathematical Relationships

Inverse Function Properties
\[\coth(\text{ACoth}(x)) = x \text{ for } |x| > 1\] \[\text{ACoth}(\coth(y)) = y \text{ for } y \neq 0\]

Identities: Fundamental inverse relationships.

Calculus Properties
\[\frac{d}{dx}\text{ACoth}(x) = \frac{1}{1-x^2}\] \[\int \text{ACoth}(x) dx = x\text{ACoth}(x) + \frac{1}{2}\ln|x^2-1| + C\]

Derivative: Rational function form.


IT Functions

Decimal, Hex, Bin, Octal conversion • Shift bits left or right • Set a bit • Clear a bit • Bitwise AND • Bitwise OR • Bitwise exclusive OR

Special functions

Airy • Derivative Airy • Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye • Spherical-Bessel-J • Spherical-Bessel-Y • Hankel • Beta • Incomplete Beta • Incomplete Inverse Beta • Binomial Coefficient • Binomial Coefficient Logarithm • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Struve table • Modified Struve • Modified Struve table • Riemann Zeta

Hyperbolic functions

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Degree to Radian • Radian to Degree