Inverse Hyperbolic Secant
Online calculator for calculating the angle to the inverse hyperbolic secant
ASech Calculator
Domain Restriction
The ASech(x) or inverse hyperbolic secant shows inverse function behavior with domain 0 < x ≤ 1.
ASech Function Curve
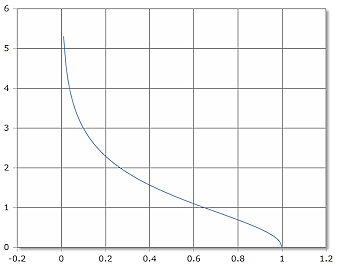
The ASech function starts at (1,0) and increases logarithmically toward infinity.
Domain: (0, 1], Range: [0, ∞)
|
|
Inverse Function Behavior of ASech
The inverse hyperbolic secant function exhibits characteristic inverse properties:
- Domain: (0, 1] (positive values up to 1)
- Range: [0, ∞) (non-negative angles)
- Starting Point: ASech(1) = 0
- Inverse: Sech(ASech(x)) = x for 0 < x ≤ 1
- Monotonicity: Strictly increasing
- Growth: Logarithmic divergence to ∞
Logarithmic Representation of ASech Function
The inverse hyperbolic secant function is expressed through logarithmic functions:
Basic Formula
Natural logarithm expression for 0 < x ≤ 1
Inverse Relation
For 0 < x ≤ 1
Formulas for the ASech Function
Definition
Natural logarithm expression for 0 < x ≤ 1
Inverse Relation
Fundamental inverse function properties
Derivative
First derivative for 0 < x < 1
Domain Restriction
Returns NaN for x ≤ 0 or x > 1
Limit Behavior
Divergent behavior as x approaches 0
Special Values
Important Values
Invalid Range
Function undefined outside (0, 1]
Starting Point
Function starts at the point (1, 0)
Properties
- Inverse function
- Strictly increasing
- Logarithmic divergence
- Domain bounded to (0, 1]
Bell Function Inverse
Relationship to inverse hyperbolic cosine
Applications
Signal processing, probability theory, bell curve analysis, inverse problems.
Detailed Description of the ASech Function
Definition and Input
The inverse hyperbolic secant function ASech(x) is the inverse function of the hyperbolic secant. It exhibits characteristic logarithmic divergence with a restricted domain.
Input
The argument must be a positive number greater than 0 and less than or equal to 1. Values outside this range return NaN (not a valid number).
Result
The result is given in degrees (full circle = 360°) or radians (full circle = 2π). The unit of measurement used is set using the Degrees or Radians menu.
Using the Calculator
Enter a value between 0 and 1 (inclusive). The ASech function calculates the angle whose hyperbolic secant equals the input value.
Mathematical Properties
Function Properties
- Domain: (0, 1] (positive values up to 1)
- Range: [0, ∞) (non-negative)
- Starting Point: ASech(1) = 0
- Monotonicity: Strictly increasing
Bell Function Inverse Properties
- Inverse of bell-shaped Sech function
- Logarithmic divergence as x → 0⁺
- Related to ACosh by reciprocal argument
- Domain restricted to positive unit interval
Applications
- Signal Processing: Bell curve analysis
- Probability Theory: Inverse bell distributions
- Mathematical Physics: Soliton theory
- Engineering: Shape analysis problems
Practical Notes
- Domain restriction: 0 < x ≤ 1 (undefined outside)
- Starting value: ASech(1) = 0
- Divergence: ASech(x) → ∞ as x → 0⁺
- Inverse relation: Sech(ASech(x)) = x for 0 < x ≤ 1
Calculation Examples
Valid Values
ASech(1) = 0
ASech(0.5) ≈ 1.317
ASech(0.1) ≈ 2.993
Special Values
ASech(1/e) ≈ 1.657
ASech(0.6) ≈ 1.074
ASech(2/3) ≈ 0.881
Invalid Inputs
ASech(0) = NaN
ASech(-0.5) = NaN
ASech(2) = NaN
Mathematical and Physical Applications
Bell Curve Analysis
Inverse Bell Functions:
Soliton pulse analysis
Shape parameter extraction
Application: Analyzing bell-shaped signals and pulses.
Probability Theory
Distribution Analysis:
Inverse probability functions
Bell-shaped distribution inversions
Example: Parameter estimation in bell distributions.
Important Mathematical Relationships
Inverse Function Properties
Identities: Fundamental inverse relationships.
Calculus Properties
Derivative: Involves reciprocal and square root.
|
|
|
|