Hyperbolic Cosecant
Online calculator for calculating the hyperbolic cosecant of an angle
Csch Calculator
Zero Exclusion
The Csch(x) or hyperbolic cosecant shows reciprocal behavior with singularity at x = 0.
Csch Function Curve
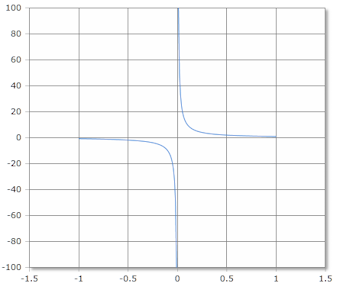
The Csch function has a vertical asymptote at x = 0 and approaches zero as x → ±∞.
Domain: ℝ \ {0}, Range: ℝ \ {0}
|
|
Reciprocal Behavior of Csch
The hyperbolic cosecant function exhibits characteristic reciprocal properties:
- Domain: ℝ \ {0} (all real numbers except 0)
- Range: ℝ \ {0} (all non-zero real numbers)
- Singularity: Vertical asymptote at x = 0
- Reciprocal: Csch(x) = 1/Sinh(x)
- Symmetry: Odd function Csch(-x) = -Csch(x)
- Asymptotes: Horizontal at y = 0
Exponential Representation of Csch Function
The hyperbolic cosecant function is expressed through exponential functions:
Basic Formula
Reciprocal of hyperbolic sine for x ≠ 0
Reciprocal Relation
Perfect reciprocal relationship
Formulas for the Csch Function
Definition
Reciprocal of hyperbolic sine for x ≠ 0
Alternative Form
Alternative exponential expressions
Derivative
Derivative involves both cosecant and cotangent
Symmetry Property
Odd function (antisymmetric)
Asymptotic Behavior
Vertical asymptote at origin, horizontal at y = 0
Special Values
Important Values
Singularity
Function has vertical asymptote at x = 0
Zero Asymptote
Function approaches zero for large arguments
Properties
- Reciprocal function
- Odd function symmetry
- Vertical asymptote at x = 0
- Horizontal asymptote at y = 0
Reciprocal Relation
Perfect reciprocal of hyperbolic sine
Applications
Quantum field theory, signal processing, soliton theory, mathematical physics.
Detailed Description of the Csch Function
Definition and Input
The hyperbolic cosecant function Csch(x) is the reciprocal of the hyperbolic sine function. It exhibits characteristic reciprocal behavior with a vertical asymptote at the origin and horizontal asymptote at zero.
Input
The angle is given in degrees (full circle = 360°) or radians (full circle = 2π). The unit of measurement used is set using the Degrees or Radians menu. Note: The function is undefined at x = 0.
Result
The result can be any non-zero real number. For large positive or negative arguments, the function approaches zero exponentially.
Using the Calculator
Enter any angle value except 0. The Csch function calculates the hyperbolic cosecant, which is the reciprocal of the hyperbolic sine.
Mathematical Properties
Function Properties
- Domain: ℝ \ {0} (all real numbers except 0)
- Range: ℝ \ {0} (all non-zero real numbers)
- Singularity: Vertical asymptote at x = 0
- Symmetry: Odd function Csch(-x) = -Csch(x)
Reciprocal Properties
- Reciprocal of hyperbolic sine function
- Vertical asymptote at x = 0
- Horizontal asymptote at y = 0
- Two separate branches on either side of x = 0
Applications
- Quantum Field Theory: Scattering amplitudes
- Soliton Theory: Nonlinear wave solutions
- Signal Processing: Pulse shape analysis
- Mathematical Physics: Special function theory
Practical Notes
- Singularity at x = 0: Function diverges to ±∞
- Zero asymptote: Approaches 0 as x → ±∞
- Odd function: Csch(-x) = -Csch(x)
- Reciprocal relation: Csch(x) = 1/Sinh(x)
Calculation Examples
Small Positive Values
Csch(0.5) ≈ 1.919
Csch(1) ≈ 0.851
Csch(2) ≈ 0.276
Negative Values
Csch(-0.5) ≈ -1.919
Csch(-1) ≈ -0.851
Csch(-2) ≈ -0.276
Asymptotic Behavior
x → 0⁺: Csch(x) → +∞
x → 0⁻: Csch(x) → -∞
x → ±∞: Csch(x) → 0
Physics and Mathematical Applications
Soliton Theory
Soliton Solutions:
u(x,t) = A·Csch(k(x-vt))
Nonlinear wave solutions
Application: Pulse propagation in optical fibers.
Quantum Field Theory
Scattering Amplitudes:
Form factors in particle physics
Feynman diagram calculations
Example: Electromagnetic form factors in QED.
Important Mathematical Relationships
Reciprocal Function Properties
Reciprocal Relationship: Perfect inverse of hyperbolic sine.
Calculus Properties
Derivative: Product of cosecant and cotangent.
|
|
|
|